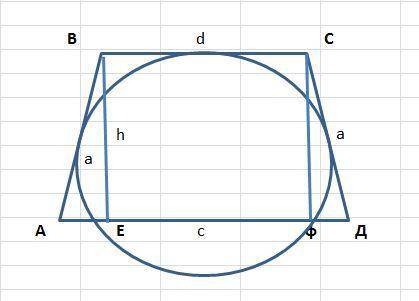
большее основание = 18 см
площадь трапеции = 60 см²
Пошаговое объяснение:
по свойству описанной трапеции r вписанного круга = h/2,где h - высота трапеции
в нашем случает h=2r = 2(d/2) = 6 (см)
теперь будем искать большее основание. для этого увидим, то большее основание равно 2АЕ + ЕФ. найдем АЕ из прямоугольного треугольника АВЕ по теореме Пифагора
АЕ =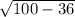 
= 8. , тогда большее основание АД=8+8+ВС
теперь по свойству описанной трапеции (сумма оснований = сумме боковых сторон) имеем ВС+ВС+16=20
вычисляем ВС = 2, тогда АД = 18
площадь трапеции S =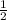 
(BC+AД)h = 60 (cм²)
1.
Обозначим объем бассейна за 1 (единицу)
1:4 = 1/4 - производительность первого насоса
1:12=1/12 - производительность второго насоса
1/4+1/12=3/12+1/12=4/12=1/3 - производительность обоих насосов
1:1/3=3 часа - время заполнения бассейна двумя насосами
2.
Обозначим путь между поселками за 1 (единицу)
1:10=1/10 - расстояние, которое проезжает первый велосипедист за 1 мин
1:15=1/15 - расстояние, которое проезжает второй велосипедист за 1 мин
1/10+1/15=3/30+2/30=5/30=1/6 - расстояние, которое проезжают оба велосипедиста за 1 мин
1:1/6=6 мин - время до встречи
3.
х - время за которое выпивает бидон молока Шарик
1:10=1/10 - часть молока, которое выпивает Матроскин за 1 час
1:х=1/х - часть молока, которое выпивает Шарикза 1 час
1:6=1/6 - часть молока, которое выпивают оба 1 час
1/10+1/х=1/6
-1/х=-1/15
-х=-15
х=15 (ч) - время за которое выпивает бидон молока Шарик
Пошаговое объяснение:
Пошаговое объяснение:
Магический квадрат – это квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу. Например (см. рисунок 1): таблица состоит из различных цифр от 1 по 9 и сумма чисел равна 15.
Другой пример (см. рисунок 2): даны всего 4 числа и нужно определить другие неизвестные числа и магический квадрат.
Для решение задачи сначала определим по известным 3 числам, в нашем примере, по числам диагонали определим сумму чисел: 21+19+17=57. Можно было определить нужную сумму чисел по известным 3 числам 2-столбца: 11+19+27=57.
Теперь нам известна сумма чисел и поэтому с её и 2 известных чисел можем определить неизвестные числа 1-строки и 3-строки:
57-21-11=25
57-27-17=13.
По известным уже числам 25 и 13 получаем другую таблицу (см. рисунок 3). Как видно из таблицы, остается найти неизвестных чисел 1-столбца и 3-столбца. Как и выше, определим их по числам столбца и с суммы:
57-21-13=23
57-25-17=15.
В итоге получаем нужную таблицу (см. рисунок 4). Можно проверить, что суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны 57.