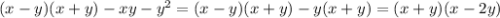
В целых числах решаем 4 системы:
1. x+y =7(1)
x-2y=1(2)
(1)-(2): 3y = 6
y = 2
x =5
2. x+y = -7(1)
x -2y = -1(2)
(1)-(2): 3y =-6
y=-2
x=-5
3. x+y = 1(1)
x-2y= 7(2)
(1)-(2): 3y=-6
y=-2
x = 3
4. x+y=-1(1)
x-2y= -7(2)
(1)-(2): 3y=6
y = 2
x =-3
Отметьте как лучший ответ, если не сложно❤️
На последнем озере село половина всех гусей и еще полгуся и оказалось, что это все летевшие гуси. Значит, полгуся — это половина всех гусей, подлетевших к последнему озеру, а всего их было 0,5·2=1 гусь. На предпоследнем озере село половина всех гусей, подлетевших к нему, и еще полгуся, а еще один гусь полетел на последнее озеро. Значит, к этому озеру подлетело (1 + 0,5)·2=3 гуся. Рассуждая таким образом дальше, получим, что к пятому озеру подлетело 7 гусей, к четвертому — 15 гусей, к третьему — 31 гусь, ко второму — 63 гуся и, наконец, к первому — 127 гусей.
И всё )!
В левой части уравнения разложим одночлены в сумму нескольких.
Число 7 является простым. Представим его в виде произведении чисел 1 и 7 или (-1) и (-7). Получаем четыре системы:
ответ: (3;-2), (5;2), (-3;2), (-5;-2).