Отметим точки E и F прямоугольника EGHF на стороне AC, а точку G и H на сторонах AB и BC соответственно. Пересечение высоты BD и отрезка GH отметим через D1.
Обозначим GH через x.
Т.к. в прямоугольнике EGHF сторона GH параллельна стороне EF, которая лежит на стороне AC треугольника ABC, то GH || AC, а следовательно ΔGBH≈ΔABC
Тогда
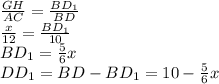
Отметим, что GE = DD1 и найдем площадь прямоугольника EGHF:
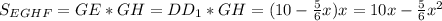
Т.е. нам надо найти максимум функции 
Для этого найдем ее производную и приравняем 0:
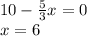
Значит x = 6 является точкой максимума функции.
Значение функции в точке максимума: 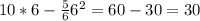
ответ: наибольшее значение площади такого прямоугольника 30 см2
Угол при вершине равнобедренного треугольника будет 30 градусов...
далее по формуле площади треугольника полупроизведение сторон на синус угла на ходишь боковые стороны, а потом по теореме косинусов находишь основание
далее чуть чуть придется провечти анализКрч,2 боковые стороны искомого треугольника будут равны половине основания большого треугольника (Т.к. боковые стороны будут медианами прямоугольных треугольников) Далее осталось найти 3 сторону...Там будут 2 подобных треугольника с коэффицентом подобия 2/sqrt(3) (коэффицент подобия находишь засчет прямоугольного треугольника с 30 и 60 углами) ну и соответственно находишь 3 сторону,а потом по формуле Герона площадь