Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была 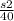 , а после встречи
, а после встречи 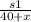 . Скорость второго пешехода до встречи и после встречи была одинаковой, значит
. Скорость второго пешехода до встречи и после встречи была одинаковой, значит  , откуда
, откуда  . У первого пешехода до встречи была скорость
. У первого пешехода до встречи была скорость  , а после встречи
, а после встречи 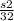 , скорость первого пешехода до встречи и после встречи была одинаковой, значит
, скорость первого пешехода до встречи и после встречи была одинаковой, значит 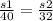 , откуда
, откуда 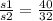 . По условию задачи составим уравнение
. По условию задачи составим уравнение .
.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была 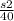 , а после встречи
, а после встречи 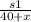 . Скорость второго пешехода до встречи и после встречи была одинаковой, значит
. Скорость второго пешехода до встречи и после встречи была одинаковой, значит  , откуда
, откуда  . У первого пешехода до встречи была скорость
. У первого пешехода до встречи была скорость  , а после встречи
, а после встречи 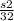 , скорость первого пешехода до встречи и после встречи была одинаковой, значит
, скорость первого пешехода до встречи и после встречи была одинаковой, значит 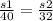 , откуда
, откуда 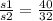 . По условию задачи составим уравнение
. По условию задачи составим уравнение .
.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
2/9
Пошаговое объяснение:
Два кубика, возможные числа:
1;2;3;4;5;6
1;2;3;4;5;6
4 задание: |a-b|=2
т.к. там модуль, то неважно, вычитаем мы очки первого из очков второго, или наоборот.
Событие верно при очках:
1;3
2:4
3:5
4;6
И наоборот.
Значит удовлетворяющих нашему условию решений - 8.
А всего вариантов - 6²=36.
Вероятность события: 8/36=2/9