№ 4. x ≤ 0.75
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4. 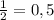
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤ 
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
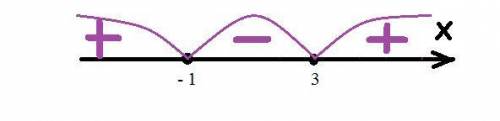
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )
Лодка двигалась по течению реки 2,5 часа с собственной скоростью 21,5 км/ч, и мы знаем скорость течения реки - 2,3 км, то вычислим расстояние, на которое успела уйти лодка. Для этого сначала выясним реальную скорость лодки, это её собственная скорость плюс скорость течения.
21,5+2,3=23,8 - скорость движения лодки по течению реки.
Теперь нужно узнать расстояние, которое лодка. Расстояние равняется скорость умноженное на время.
23,8×2,5=59,5 км - расстояние, которое лодка.
Чтобы вернуться, ей надо пройти такое же расстояние обратно. Чтобы узнать, с какой скоростью лодка двигается против течения, нужно от собственной скорости лодки отнять скорость течения:
21,5-2,3=19,2 км/ч - скорость лодки против течения.
Теперь узнаем, сколько километров пройдёт лодка за 3,1 часа обратного пути:
19,2×3,1=59,52
Мы видим, что это как раз то расстояние, на которое ушла лодка.
ответ: да, за 3,1 часа лодка успеет вернуться в порт.