Question

Вершина параболы y=ax^2+bx+c имеет координаты x=6,y=-12. зная, что ветви параболы направлены вверх и функция имеет один из нулей при x=8, найти a, b и c. , можно только ответ, но желательно с решением​

Answer 1

ответ: a = 3, b = -36, c = 96.

Пошаговое объяснение:

y(8)=0,  64a+8b+c=0.  (1)

y(6)=-12, 36a+6b+c=-12. (2)

Из уравнения (1) вычтем уравнение (2): 28a+2b=12;   14a+b=6 ⇒ b = 6 - 14a. (3)

Вернемся к координатам вершины: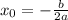 $x_0=-\frac{b}{2a}$.

Вместо b подставляем равенство (3):

$-\frac{6-14a}{2a} =6,\Rightarrow 14a-6=12a, 2a=6\Rightarrow a=3.$

Можем найти b: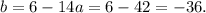 $b = 6-14a=6-42=-36.$.

Чтобы найти с, подставим найденные значения а и b, к примеру, в уравнение (1):

$64a+8a+c=0,\\192-288=-c,\\-c=-96\Rightarrow c=96.$