Question

Известно, что при бросании десяти игральных костей выпала хотя бы одна единица. какова вероятность p того, что выпало две или более единиц?

Answer 1

ответ: $\displaystyle \frac{6^{10}-3 \cdot {5^{10}}}{6^{10}-5^{10}}$  Решение:

Р (выпала хотя бы одна единица) = 1 - Р (выпало ни 1 единицы) =

= $1 - \bigg(\dfrac{5}{6}\bigg)^{10}$

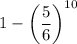
Р (выпало 2, 3, ... ,10 единиц) = 1 - Р (выпало 0 или 1 единица) =

= $1-\dfrac{5^{10}}{6^{10}} - 10 \cdot \dfrac{1}{6} \cdot \dfrac{5^9}{6^9} = 1 - 1\cdot\dfrac{5^{10}}{6^{10}} - 2 \cdot \dfrac{5^1^0}{6^1^0} = 1 - 3 \cdot \dfrac{5^{10}}{6^{10}}.$

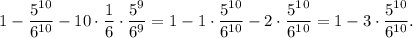
Р (пересечение) = Р(выпало 2, 3, ... ,10 единиц) =

= $1 - 3 \cdot \dfrac{5^{10}}{6^{10}}.$

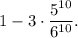
Р (выпало 2 или более единиц | выпала хотя бы одна единица) =

= $\displaystyle \frac{1-3 \cdot \dfrac{5^{10}}{6^{10}} }{1-\dfrac{5^{10}}{6^{10}} } = \frac{6^{10}-3 \cdot {5^{10}} }{6^{10}} \cdot \frac{6^{10}}{6^{10}-5^{10}} =\frac{6^{10}-3 \cdot {5^{10}} }{6^{10}-5^{10}}$

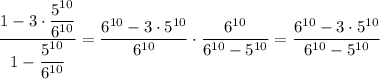
При решении мы пользовались формулой условной вероятности:

$P (A|B)=\dfrac{P(A \cap B)}{P(B)}$