Вначале посчитаем (перечислим), сколько всего исходов может быть, если на всех трех кубиках выпали разные грани. Это будет несложно сделать, если мы будем считать, что порядок значения не имеет (если же мы будем считать, что порядок имеет значение, то получим тоже самое).А потом посчитаем, в скольких из этих присутствует единица.Найдем отношение второго к первому, то есть вероятность.
Итак, перечислим исходы, если на всех кубиках выпало разное число очков, без учета порядка:
123, 124, 125, 126, 134, 135, 136, 145, 146, 156,
234, 235, 236, 245, 246, 256, 345, 346, 356, 456.
В первой строке - все исходы, в которых выпадает 1; их всего 10. Во второй строке оставшиеся исходы, их тоже 10.
Значит:
Р (выпала единица | на всех трёх костях выпали разные грани) =
=
Задача решена!
P.S. Задачу можно решить целиком через условную вероятность, как я сделала вначале, но это значительно скучнее, чем так. И результаты, кажется, совпадают.
47-простое число, имеет два делителя 1 и само себя, то есть 47 117=3*39 то есть наибольший 39 291=3*97 133=7*19 79-79 простое 109 простое 87=3*29 78=2*39 67 38=2*19 23 89 161=7*23 72=2*36 113 231=3*77 169=13*13 98=2*48 149 74=2*37 121=11*11 139 107 97 235=5*47 171=3*57 34=2*17 138=2*69
самый простой получить наибольший делитель, поделить число на 2, потом на 3. в большинстве случаев он и появится, если нет, то делить на последующие простые числа: 5,7,11,13,17,19, есть таблица с простыми числами, по ней можно отсеять сразу те, которые имеют только два делителя единицу и себя.
Трапеция АВСД, высота ВН пересекает диагональ АС в точке О, при этом ВО =10, ОН=8.; АВ =ВС=х по условию, значит треугольники АОН и СОВ подобны по двум углам (так как угол ВАС =углу ВСА и углы при вершине О равны как вертикальные) Из подобия треугольников следует пропорция ВС/АН=ВО/ОН, т.е х/АН=10/8,значит АН= 4х/5 и всё нижнее основание АД= 4х/5+х+4х/5, т.е АД=13х/5. Но из прямоугольного треугольника АВН по теореме Пифагора АВв квадрате = АН в квадрате + ВН в квадрате, т.е Х в квадрате = (4х/5)в квадрате + 18 в квадрате. Отсюда х=30. Тогда Верхнее основание ВС=30,нижнее АД= 13х/5=78 и площадь трапеции равна полусумме оснований умножить на высоту, т.е (78+30)/2 и умножить на 18, получится 972 ответ : 972
Составим "порядок действий" к задаче:
Вначале посчитаем (перечислим), сколько всего исходов может быть, если на всех трех кубиках выпали разные грани. Это будет несложно сделать, если мы будем считать, что порядок значения не имеет (если же мы будем считать, что порядок имеет значение, то получим тоже самое).А потом посчитаем, в скольких из этих присутствует единица.Найдем отношение второго к первому, то есть вероятность.Итак, перечислим исходы, если на всех кубиках выпало разное число очков, без учета порядка:
123, 124, 125, 126, 134, 135, 136, 145, 146, 156,
234, 235, 236, 245, 246, 256, 345, 346, 356, 456.
В первой строке - все исходы, в которых выпадает 1; их всего 10. Во второй строке оставшиеся исходы, их тоже 10.
Значит:
Р (выпала единица | на всех трёх костях выпали разные грани) =
=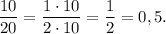
Задача решена!
P.S. Задачу можно решить целиком через условную вероятность, как я сделала вначале, но это значительно скучнее, чем так. И результаты, кажется, совпадают.