245,3 см² полная площадь цилиндра
Пошаговое объяснение:
По условию задания дано: D = 6,2 см, h = 9,5 см
D = 2R, R = D/2 = 6,2/2 = 3,1 см
Полная площадь поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра + удвоенная площадь основания: S = 2 πRh + 2 πR²
Площадь боковой поверхности круглого цилиндра равна произведению длины окружности основания на его высоту:
S = 2πRh = 2*3,14*3,1*9,5 ≈ 184,95 см² - площадь боковой поверхности
Основание - это круг. Площадь круга вычисляется по стандартной формуле: S = 2 πR² = 2*3,14*3,1² ≈ 60,35 см²
Вычислим общую площадь поверхности цилиндра:
S = 184,95 + 60,35 ≈ 245,3 см² - полная площадь цилиндра
Можно вычислить и так:
S = 2πR(h+R) = 2*3,14*3,1(9,5 + 3,1) ≈ 245,3 см² - полная площадь цилиндра
Эллипс.
Эллипс с каноническим уравнением
x2
a2
+
y2
b2
=1,a≥b>0, имеет форму изображенную на рисунке.
Параметры a и b называются полуосями эллипса (большой и малой соответственно). Точки A1(−a,0), A2(a,0), B1(0,−b), и B2(0,b), его вершинами. Оси симметрии Ox и Oy - главными осями а центр симметрии O− центром эллипса.
Точки F1(−c,0) и F2(c,0), где c=
√
a2−b2
≥0, называются фокусами эллипса векторы
¯
F1M
и
¯
F2M
− фокальными радиус-векторами, а числа r1=|
¯
F1M
| и r2=|
¯
F2M
|− фокальными радиусами точки M, принадлежащей эллипсу. В частном случае a=b фокусы F1 и F2 совпадают с центром, а каноническое уравнение имеет вид
x2
a2
+
y2
a2
=1, или x2+y2=a2, т.е. описывает окружность радиуса a с центром в начале координат.
Число e=
c
a
=
√
1−
b2
a2
(0≤e<1) называется эксцентриситетом эллипса и является мерой его "сплюснутости" (при e=0 эллипс является окружностью.)
Прямые D1:x=−a/e и D2:x=a/e, перпендикулярные главной оси и проходящей на расстоянии a/e от центра, называются директрисами эллипса.
Теорема. (Директориальное свойство эллипса)
Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно e.
Примеры.
2.246. Построить эллипс 9x2+25y2=225. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Пошаговое объяснение:
я не знаю правильно ли это
Пошаговое объяснение:
Для решения данной задачи требуется составить систему линейных уравнений. Пусть x - собственная скорость катера, а y - скорость течения.
Тогда получим следующее:
x + y - это будет скорость катера по течению.
x - y - это будет скорость катера против течения.
Имеем:

Раскрываем скобки:

Теперь уравняем переменные в системе:
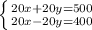
Уничтожаем 20y и -20y путем сложения.
Получаем:
40x = 900
x = 22,5 км/ч - собственная скорость. (Т.к. мы соб.скорость приняли за x)
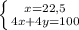



ответ: собственная скорость катера - 22,5 км/ч. А скорость течения - 2,5 км/ч
бокоаая поверхность цилиндра равна произведению длины окружности основания и высоты :
Sбок.=2пиrh
Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований.
Sпол.пов.=Sбок.+2Sосн.
Sпол.пов.=2пиrh+2пиr^2=2пиr(h+r)
d=6,2см ; d=2r ; r=3,1см
h=9.5см
Sпол.пов.=(2*пи*3,1*9,5)+(2*пи*(3,1)^2)=58,9пи+19,22пи=78,12пи см^2