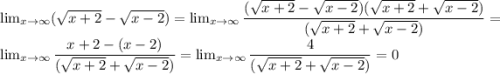
0
Пошаговое объяснение:
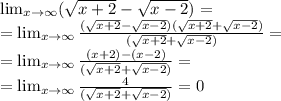
5/Задание № 3:
На доске были записаны 10 последовательных натуральных чисел. Когда стёрли одно из них, то сумма девяти оставшихся получилась 2017. Какое число стёрли?
РЕШЕНИЕ: Найдем сумму 10 чисел: х+х+1+х+2+х+3+х+4+х+5+х+6+х+7+х+8+х+9=10х+45
Если вычеркнули наименьшее число, то сумма стала 9х+45, если вычеркнули наиболее число, то сумма стала 9х+36.
Значит, число 2017 с одной стороны не меньше 9х+36, с другой стороны не больше 9х+45.
9х+36<=2017
9х<=1981
х<=220+1/9
9х+45>=2017
9х>=1972
х>=219+1/9
Значит, х=220.
Сумма 10 чисел: 10х+45=10*220+45=2245
Вычеркнутое число 2245-2017=228
ОТВЕТ: 228
√(4-10х-х²)=-2х-1 ;
Возведем в квадрат обе части
(4-10х-х²)=(-2х-1)²
4-10х-х²=4х²+4х+1
5х²+14х-3=0
х₁,₂=(-7±√(49+15))/5=(-7±8)/5
x₁=-3; x₂=1/5
При возведении в квадрат могли появиться посторонние корни. Поэтому сделаем проверку.
x₁=-3; √(4-10*(-3)-9)=-2*(-3)-1 ; 5=5, значит, x₁=-3 -корень исходного уравнения. Второй корень не является корнем исходного уравнения, т.к. правая часть √(4-10х-х²)=-2х-1 при х=1/5 - есть число отрицательное, чего быть не может, т.к. левая часть не может быть отрицательной.
Значит, корень один. И он равен -3.
ответ -3