Согласитесь, что удаление с факультатива всего 1 (одного) болтуна, не уменьшит класс наполовину! И число учеников в классе будет больше половины. Ведь даже при таком, минимальном раскладе числа учеников в классе: 2 болтуна + 1 молчун=3 ученика. 3-1=2⇒ 2 больше чем 3/2.
Рассуждаем так: если перед началом проведения факультатива, из всего числа учеников, количество находящихся в нём болтунов нечётно- то, вообще никого не надо удалять, ведь по условию задания , болтуны в этом случае молчат. Но если перед началом проведения факультатива, число болтунов чётно- то надо одного болтуна удалить с занятия, чтобы число болтунов стало нечётным, и тогда все будут трудиться на уроке без излишней болтовни.
Пошаговое объяснение:
Вероятность того, что первый вызванный студент готов к семинару равна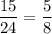 . В группе остается 23 студента из них 14 готовые. Вероятность того, что второй вызванный студент готов к семинару равна
. В группе остается 23 студента из них 14 готовые. Вероятность того, что второй вызванный студент готов к семинару равна 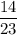 . Аналогично, вероятность того, что третий вызванный студент готов к семинару равна
. Аналогично, вероятность того, что третий вызванный студент готов к семинару равна 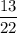 . По теореме умножения, вероятность того, что вызванные наугад 3 студента готовы к семинару равна
. По теореме умножения, вероятность того, что вызванные наугад 3 студента готовы к семинару равна 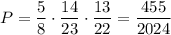
ответ: P = 455/2024.