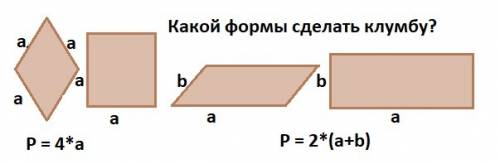
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
На момент каждой n-ой встречи гонщики в сумме проезжают n целых кругов. Значит к моменту 7-ой встречи они проехали в сумме 7 целых кругов, каждый проехал целое количество кругов. Так как первый тратил на каждый круг на 30 секунд меньше, то он проехал больше кругов, чем второй.
Возможны варианты:
1) первый проехал 4 круга, второй 3;
2) первый проехал 5 кругов, второй 2;
3) первый проехал 6 кругов, второй 1.
Рассмотрим их все:
1) пока первый проезжает 1 круг, второй проезжает 3/4 круга. Значит второй проезжает оставшуюся 1/4 круга за 30 секунд, а весь круг за 30:1/4 = 30·4 = 120 секунд. Тогда встреча произошла через 120·3 = 360 секунд после старта;
2) пока первый проезжает один круг, второй проезжает 2/5 круга. Значит второй проезжает оставшиеся 3/5 круга за 30:3/5 = 30:3·5 = 10·5 = 50 секунд. Тогда встреча произошла через 50·2 = 100 секунд после старта;
3) пока первый проезжает один круг, второй проезжает 1/6 круга. Значит второй проезжает оставшиеся 5/6 круга за 30:5/6 = 30:5·6 = 6·6 = 36 секунд. Тогда встреча произошла через 36·1 = 36 секунд после старта.