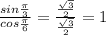Наименьшее значение косинуса равно -1, так как на единичной окружности наименьшее значение х равно -1 (точка с наименьшей абсциссой находится слева, в α = π).
Наибольшее значение косинуса равно 1, поскольку наибольшее значение x на единичной окружности равно 1 (оно достигается справа, в α = 0).
Следовательно, область значений косинуса — промежуток [-1;1].
1) длина прямоугольника 13 см ширина на 1 дм меньше, 1 дм=10 см , значит 13-10=3 (см) ширина прямоугольника можем найти периметр прямоугольника Рпрям=13+13+3+3=32 (см) у квадрата все стороны равны, а периметр такой же, найдем сторону квадрата 32:4=8 (см) теперь можем найти площадь квадрата S=8*8=64 (см)
решение можно записать так: 1 дм=10 см 13-10=3 (см) ширина прямоугольника 13+13+3+3=32 (см) периметр прямоугольника 32:4=8 (см) сторона квадрата 8*8=64 (см²) ответ: площадь квадрата 64 см²
1) длина прямоугольника 13 см ширина на 1 дм меньше, 1 дм=10 см , значит 13-10=3 (см) ширина прямоугольника можем найти периметр прямоугольника Рпрям=13+13+3+3=32 (см) у квадрата все стороны равны, а периметр такой же, найдем сторону квадрата 32:4=8 (см) теперь можем найти площадь квадрата S=8*8=64 (см)
решение можно записать так: 1 дм=10 см 13-10=3 (см) ширина прямоугольника 13+13+3+3=32 (см) периметр прямоугольника 32:4=8 (см) сторона квадрата 8*8=64 (см²) ответ: площадь квадрата 64 см²
а) может
б) может
в) не может
г) может
Пошаговое объяснение:
Наименьшее значение косинуса равно -1, так как на единичной окружности наименьшее значение х равно -1 (точка с наименьшей абсциссой находится слева, в α = π).
Наибольшее значение косинуса равно 1, поскольку наибольшее значение x на единичной окружности равно 1 (оно достигается справа, в α = 0).
Следовательно, область значений косинуса — промежуток [-1;1].
а)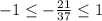 - верно
- верно
б)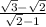 ≈ 0,7
≈ 0,7
в)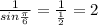
г)