Задание 1. Даны матрицы A,B,C.
1) В матрице A,B найти определитель;
2) Вычислить A-C
1)
7 2 4
det A = -3 9 -2 =
2 1 5
= 7·9·5 + 2·(-2)·2 + 4·(-3)·1 - 4·9·2 - 7·(-2)·1 - 2·(-3)·5 = 315 - 8 - 12 - 72 + 14 + 30 = 267
1 2 -4
det B= 6 5 1 =
-2 0 3
= 1·5·3 + 2·1·(-2) + (-4)·6·0 - (-4)·5·(-2) - 1·1·0 - 2·6·3 = 15 - 4 + 0 - 40 - 0 - 36 = -65
2) Решение и ответ на фото
Задание 2. Решить систему уравнений методом Гаусса. Решение на фото. Если подробно написать объяснение решений, это будет очень долго. И мне нравится метод Гаусса, сложно решать.
{x1 + x2 + x3 = 4
{5x1 + 3x2 + 2x3 = 1
{3x1 + 2x2 + 3x3 = -1
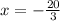
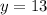
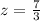
Задание 3.
Найдите производные следующих функций:
1)y=11x⁵+11
y'=55x⁴+0=55x⁴
2)
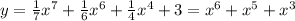
3 и 4, я не знаю как решить( поэтому оставлю как есть
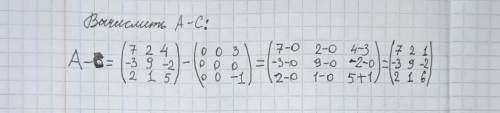
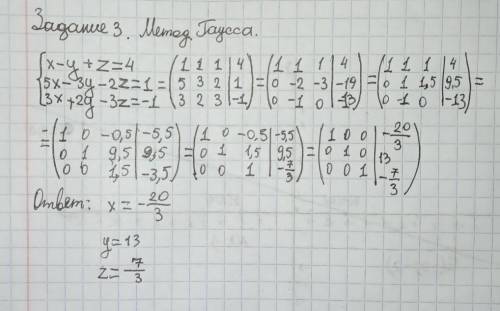
* На "5" без остатка делятся числа, которые заканчиваются на цифры "5" и "0".
* На "9" без остатка делятся числа, сумма цифр в которых делится без остатка на "9".
* На "3" без остатка делятся числа, сумма цифр которых делится без остатка на "3".
А теперь нужно выбрать числа, в которых совпадают все четыре вышеперечисленных условия. Это числа, которые заканчиваются на "0" и сумма цифр в которых делится без остатка на 9:
* наименьшее - 100.080: * наибольшее - 999.990:
100.080 : 3 = 33.360 999.990 : 3 = 333.330
100.080 : 5 = 20.016 999.990 : 5 = 199.998
100.080 : 9 = 11.120 999.990 : 9 = 111.110
100.080 : 10 = 10.008 999.990 : 10 = 99.990