Эксцентриситетом эллипса называют отношение ε = c/a , которое может принимать значения в пределах 0 ≤ x < 1.
В нашем случае: ε = 2/3.
Для построения графика удобнее преобразовать уравнение относительно у:
(y+1)²/(√5)² = 1 - ((x-3)²/3²),
(y+1)² = 5 - 5√(1 - ((x-3)²/3²)),
у = +-(√5 - 5((x-3)²/3²)) - 1.
Уравнение с плюсом определяет верхнюю дугу эллипса, с минусом
– нижнюю дугу эллипса.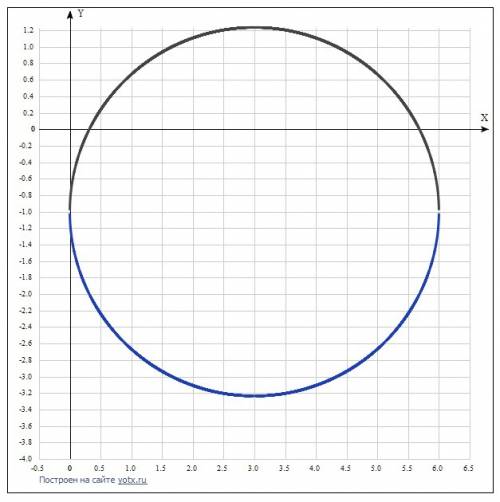
Пошаговое объяснение:
v(t) = 6t² + 18t
v(4) = 96 + 72 = 168
a(t) = 12t + 18
a(4) = 48 + 18 = 66
45.
y = f(x0) + f'(x0)(x-x0)
f(-3) = 9 - 15 = -6
f'(x) = 2x + 5
f'(-3) = -6 + 5 = -1
y = -6 - (x + 3) = -x - 9