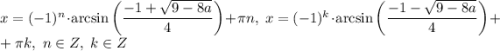1) 0.3х-0.6=0.6+0.2х+0.8 переносим 0.3х-0.2х=0.6+0.6+0.8 0.1х=2 х=2 2)Возьмём меньшую корзину за х => большая корзина = 3х Также из условия мы знаем что х+25=3х-15 находим х-3х=-25-15 -2х=-40 2х=40. х=20 3х=60 3)возьмём за х-большее число за у - меньшее. Из условия мы знаем у+33=х также мы знаем 30%х=2/3у из этого 0.3х=2/3у. используя у+33=х возьмём 0.3(у+33)=2/3у из этого путём вычислений 0.3у+9.9=2/3у. переносим -20/30у+9/30у=-9.9 -11/30у=-9.9 у=(9.9/11)*30=27 х равен 27+33=50 4) Что значит ??? 5) где переменная к которой искать корни??
1) 0.3х-0.6=0.6+0.2х+0.8 переносим 0.3х-0.2х=0.6+0.6+0.8 0.1х=2 х=2 2)Возьмём меньшую корзину за х => большая корзина = 3х Также из условия мы знаем что х+25=3х-15 находим х-3х=-25-15 -2х=-40 2х=40. х=20 3х=60 3)возьмём за х-большее число за у - меньшее. Из условия мы знаем у+33=х также мы знаем 30%х=2/3у из этого 0.3х=2/3у. используя у+33=х возьмём 0.3(у+33)=2/3у из этого путём вычислений 0.3у+9.9=2/3у. переносим -20/30у+9/30у=-9.9 -11/30у=-9.9 у=(9.9/11)*30=27 х равен 27+33=50 4) Что значит ??? 5) где переменная к которой искать корни??
Замена: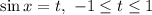
Данное уравнение будет иметь корни, если , то есть
, то есть 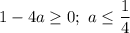
Имея два действительных корня, определим, при каких выполняется неравенство
выполняется неравенство 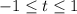
Учитывая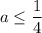 , имеем:
, имеем: ![a \in \bigg[-2; \dfrac{1}{4} \bigg]](/tpl/images/1054/0118/1ef46.png)
Учитывая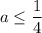 , имеем:
, имеем: ![a \in \bigg[0; \dfrac{1}{4} \bigg]](/tpl/images/1054/0118/d8d0e.png)
Обратная замена:
ответ: если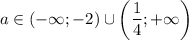 , то уравнение не имеет корней; если
, то уравнение не имеет корней; если 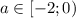 , то
, то 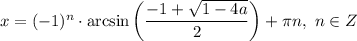 ; если
; если ![a \in \bigg[0; \dfrac{1}{4} \bigg]](/tpl/images/1054/0118/d8d0e.png) , то
, то 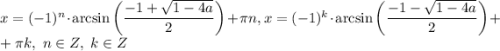
Решаем аналогично:
Замена: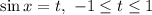
Учитывая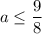 , имеем:
, имеем: ![a \in \bigg[-2; \dfrac{9}{8} \bigg]](/tpl/images/1054/0118/856ab.png)
Учитывая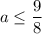 , имеем:
, имеем: ![a \in \bigg[0; \dfrac{9}{8} \bigg]](/tpl/images/1054/0118/76212.png)
Обратная замена:
ответ: если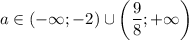 , то уравнение не имеет корней; если
, то уравнение не имеет корней; если 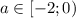 , то
, то 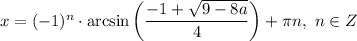 ; если
; если ![a \in \bigg[0; \dfrac{9}{8} \bigg]](/tpl/images/1054/0118/76212.png) , то
, то