1) 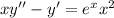
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на 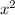 , получаем
, получаем
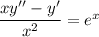
В левой части уравнения это ни что иное как формула производной частного, то есть :
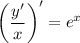
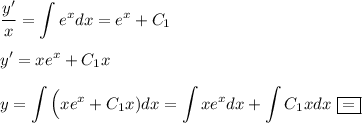
Подсчитаем отдельный интеграл 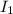 по частям.
по частям.
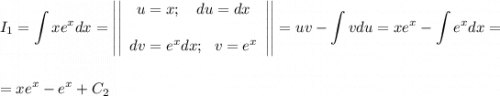
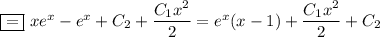
2) 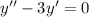
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена 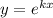 , перейдём к характеристическому уравнению:
, перейдём к характеристическому уравнению: 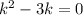 ,
, 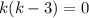 корни которого
корни которого 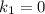 и
и 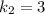 . Тогда общее решение диф. уравнения:
. Тогда общее решение диф. уравнения: 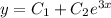 и его первая производная
и его первая производная 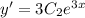 .
.
Осталось найти константы C₁ и C₂ , подставляя начальные условия.
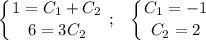
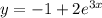 — частное решение.
— частное решение.
1й - 30 минут, 2й - 24 минуты
Пошаговое объяснение:
Пусть
Скорость 1 пешего вторую половину дороги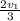
С информации про 1 пешего получаем:
С информации про 2 пешего получаем:
По дополнительному условию из вопроса получаем, что 1 пеший потратил на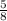 пути столько же времени, что и 2 пеший.
пути столько же времени, что и 2 пеший.
Проанализируем этот участок дороги.
Первый пеший шел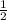 пути с более высокой скоростью, остальные
пути с более высокой скоростью, остальные 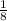 с более низкой.
с более низкой.
Времени он потратил
Второй пеший за вторую половину времени бОльшее расстояние, чем за первую. На отрезке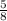 пути он уже шёл с повышенной скоростью. Для него аналогичный отрезок пути посчитаем как общее время пути без последних
пути он уже шёл с повышенной скоростью. Для него аналогичный отрезок пути посчитаем как общее время пути без последних 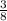 пути
пути
Времени потратил 2 пеший
Получаем систему, где t измеряется в минутах:
Находим