Пусть собств. скорость / км/ч/, тогда по течению скорость составила х+9, а против течения х-9
24/(х+9)=24/(х-9)=5
общий знаменатель (х+9)*(х-9) х не равен плюс или минус девяти. Приведем дроби к общему знаменателю. 24*(х+9+х-9)=5(х²-81), раскроем скобки, соберем все с одной стороны, приведем подобные и выйдем на квадратное уравнение.
5х²- 48х- 405=0, х₁,₂=(24±√(576+405*5))/5=(24±√2601)/5
(24±51)/5; х₁=15, х₂<0, не имеет смысла. Значит, собственная скорость лодки равна 15 км/час
ответ 15 км/ч
Подробнее - на -
Пошаговое объяснение:
Бесконечно длинных арифметических прогрессий состоящих только из степеней не существует. Докажем это. Пусть есть прогрессия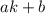 , где
, где 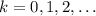 Пусть НОД
Пусть НОД 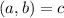 . Перепишем нашу прогрессию так:
. Перепишем нашу прогрессию так:
Поэтому, скорее всего имеются в виду прогрессии любой наперед заданной длины. Они как раз существуют. Покажем, как построить такую прогрессию. Будем пытаться сделать прогрессию длины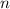 такого вида:
такого вида:
т. е. некоторое число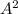 умножается на натуральный ряд:
умножается на натуральный ряд:
Видно, что в этом случае первый член являтся второй степенью. Потребуем также, чтобы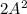 было 3-ей степенью,
было 3-ей степенью, 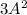 было 5-ой степенью, и так далее:
было 5-ой степенью, и так далее: 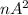 - степень с показателем
- степень с показателем 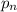 - n-ым простым числом.
- n-ым простым числом.
Представим число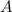 в виде
в виде
Возьмем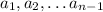 такие, что
такие, что
и
В этом случае для любого натурального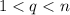
Из построения мы знаем, что все
мы знаем, что все 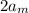 кроме
кроме 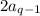 делятся на
делятся на 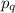 . Но
. Но
Таким образом доказано, что все показатели степеней в разложении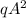 делятся на
делятся на 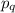 а это означает, что
а это означает, что
Указанным выше можно построить сколь угодно длинную арифметическую прогрессию, состоящую только из степеней.