ответ: я в своем познании настолько преисполнился, что я как будто бы уже сто триллионов миллиардов лет проживаю на триллионах и триллионах таких же планет, как эта земля. мне этот мир абсолютно понятен, и я здесь ищу только одного - покоя, умиротворения и вот этой гармонии, от слияния с бесконечно вечным, от созерцания великого фрактального подобия и от вот этого замечательного всеединства существа, бесконечно вечного, куда ни посмотри, хоть вглубь - бесконечно малое, хоть ввысь - бесконечное большое, понимаешь? а ты мне опять со своим вот этим, иди суетись дальше, это твоё распределение, это твой путь и твой горизонт познания и ощущения твоей природы, он несоизмеримо мелок по сравнению с моим, понимаешь? я как будто бы уже давно глубокий старец, бессмертный, ну или там уже почти бессмертный, который на этой планете от её самого зарождения, ещё когда только солнце только-только сформировалось как звезда, и вот это газопылевое облако, вот, после взрыва, солнца, когда оно вспыхнуло, как звезда, начало формировать вот эти коацерваты, планеты, понимаешь, я на этой земле уже как будто почти пять миллиардов лет живу и знаю её вдоль и поперёк этот весь мир, а ты мне какие-то люки показываешь, листья эти, ремонты. я в своем познании настолько преисполнился, что я как будто бы уже сто триллионов миллиардов лет проживаю на триллионах и триллионах таких же планет, как эта земля.
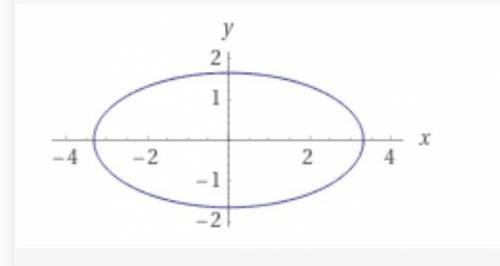
Дан эллипс 4х² + 16у² = 44. Из уравнения видно, что центр его находится в начале координат.
Выразим его уравнение в каноническом виде, разделив обе части на 44: (4х²/44) + (16у/44) = 44/44.
(х²/11) + (у²/(11/4)) = 1.
Отсюда получаем длины полуосей: a = √11, b = √11/2.
Фокусы находятся на расстоянии "с" от центра.
с = √(a² - b²) = √(11 - (11/4) = √33/2.
Эксцентриситетом эллипса е = с/а = (√33/2)/√11 = √33/(2√11).
Прямые D1:x=−a/e и D2:x=a/e, перпендикулярные главной оси и проходящей на расстоянии a/e от центра, называются директрисами эллипса. D: x = +-(√11)/(√33/(2√11)) = +-(22/√33).
1)
{x^2+2y^2=18,x^2-2y^2=14 <=>{x^2+2y^2=18,2x^2=32 <=>{x^2+2y^2=18,x^2=16 <=>{x^2+2y^2=18,x=4 <=>{16+2y^2=18,x=4 <=>{2y^2=2,x=4 <=>{y^2=2/2,x=4 <=>{y=1,x=4
2)
{y=x^2+4,x^2+y^2=49 <=>{x^2=y-4,y-4+y^2=49 <=>{x^2=y-4,y^2+y-4-49=0 <=>{x^2=y-4,[y^2+y-53=0,d=1-4*1*(-53)=213,y1=-1-sqrt213/2,y2=-1+sqrt213/2 <=>{x^2=-1+sqrt213/2-4,y=-1+sqrt213/2 <=>{x=sqrt[-1+sqrt213/2-4],y=-1+sqrt213/2