Математика: Напишите решение уравнения: - 5.3:a-3.18=-3.78

Напишите решение уравнения: - 5.3:a-3.18=-3.78

👇

Увидеть ответ

Ответ:

Айгульнафис

15.05.2021

-5,3 : а — 3,18 = — 3,78

-5,3 : а = — 3,78 + 3,18

-5,3 : а = — 0,6

a = (-5,3) : (-0,6)

a = 8⁵/₆

Проверка

-5,3 : 8⁵/₆ — 3,18 = — 3,78

-⁵³/₁₀ : ⁵³/₆ — 3,18 = — 3,78

-⁵³/₁₀ × ⁶/₅₃ — 3,18 = — 3,78

-⁵³ˣ⁶/₁₀ₓ₅₃ — 3,18 = — 3,78

-⁶/₁₀ — 3,18 = — 3,78

-0,6 — 3,18 = — 3,78

-3,78 = — 3,78

Пошаговое объяснение:

4,8(65 оценок)

Открыть все ответы

Ответ:

Shatunova1976

15.05.2021

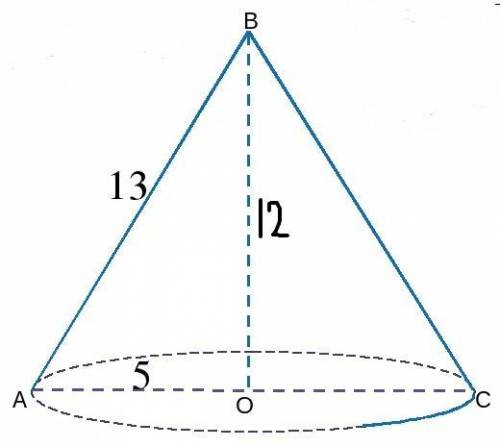
Высота конуса 12 см,диаметр основания 10 см. найдите площадь боковой поверхности конуса.

Площадь боковой поверхности конуса находим по формуле:

S бок. = ПRl, где R - радиус основания конуса, L - длина его образующей.

Найдем образующую конуса АВ по теореме Пифагора:

АВ² = ВО² + АО²

АО - радиус основания. Радиус равен половине диаметра. Т.е АО = 5 см.

Тогда:

АВ² = 5² + 12²

АВ² = 25 + 144

АВ² = 169

АВ = 13

Значит АВ = 13 см.

Поставим имеющиеся значения и найдем искомую величину:

S(бок) = п * 5 * 13 = 65п (см²)

ответ: 65п (см²)

Высота конуса 12 см,диаметр основания 10 см. найдите площадь боковой поверхности конуса.

4,5(17 оценок)

Ответ:

seanius

15.05.2021

"Das Auto ist kein Luxus, sondern ein Fortbewegungsmittel," - diese Worte von den bekannten Werken von Ilf und Petrow, ironisch klang, in unserer Zeit gewonnen ein echtes Gefühl, mehr als 10 Millionen Menschen in der Welt haben ein Auto für den persönlichen Gebrauch..Natürlich hat Straßenverkehr einen wichtigen Platz im Leben des Menschen. Es trägt mehr als 80% von Wirtschaftsgütern, auf Grund der hohen Wendigkeit des Straßenverkehrs, die Möglichkeit, Waren zu liefern "Tür zu Tür" ohne Zusatzlasten auf dem Weg, und deshalb Hochgeschwindigkeits-Lieferung und Ladungssicherung.
Eine große Länge der Autobahnen ermöglicht die weitverbreitete Anwendung in einer großen Tragfähigkeit.Hohe Mobilität, die Fähigkeit, schnell auf Änderungen in Straßenpersonenverkehr reagieren setzen "außer Konkurrenz" in der Organisation des Personennahverkehrs. Auf sie entfallen nahezu die Hälfte des Personenverkehrs.Der Straßenverkehr hat eine große Rolle bei der Gestaltung der Charakter der modernen Siedlung, Verbreitung weit Tourismus, territorialen Dezentralisierung der Industrie und im Dienstleistungssektor gespielt. Von in die Atmosphäre Hunderten von Millionen von Tonnen gefährlicher Stoffe emittierten Abgasen jährlich;: Zur gleichen Zeit hat es viele negative Phänomene verursacht Auto - einer der Hauptfaktoren, der Lärmbelastung; Straßen, vor allem in der Nähe von Stadtzentren, "frisst" wertvoller landwirtschaftlicher Flächen. Unter dem Einfluss der schädlichen Auswirkungen des Straßenverkehrs Verschlechterung der Gesundheit, vergiftete Böden und Gewässern leiden die Flora und Fauna.
Der Parkplatz, der eine der ist, vor allem in den Städten konzentriert. Wenn der Weltdurchschnitt von 1 km2 gibt es fünf Autos, deren Dichte in den großen Städten der Industrieländer in den 200 bis 300-mal höher.Mit der Entwicklung der Städte und das Wachstum der städtischen Zentren noch dringlicher geworden zeitnahe und hochwertige Dienstleistungen für die Bevölkerung, den Schutz der Umwelt vor den schädlichen Auswirkungen auf die Stadt, vor allem der Automobil- und Transport.Autos brennen eine riesige Menge an Öl, während die zu erheblichen Schäden für die Umwelt, vor allem die Atmosphäre. Da der Großteil der Autos in Städten und größeren Städten konzentriert, die Luft in diesen Städten nicht nur von sauerstoffarmen, sondern auch von schädlichen Abgaskomponenten verschmutzt. Laut Statistik in den Vereinigten Staaten, alle Verkehrsträger stellen 60% der Gesamtmenge der Schadstoffe in die Luft, der Industrie veröffentlicht - 17% Energie - 14%, andere - 9% ist für die Beheizung von Gebäuden und anderen Einrichtungen, und Entsorgung.
Die Widersprüche, von denen "gewebt" Auto vielleicht nichts gekommen war, um so stark wie in den Schutz der Natur zu beleuchten. Auf der einen Seite ist es einfacher für das Leben eines Mannes, auf der anderen - es vergiftet im wahrsten Sinne des Wortes. Fachleute haben festgestellt, dass ein Fahrzeug aus der Atmosphäre absorbiert jährlich in durchschnittlich mehr als 4 Tonnen Sauerstoff, die Auspuffgase emittieren von etwa 800 kg von Kohlenmonoxid, etwa 40 kg von Stickoxiden und etwa 200 kg aus verschiedenen Kohlenwasserstoffen. Wenn Sie diese Zahlen multiplizieren mit 400 Millionen. Einheiten der weltweit Fuhrpark, kann man sich vorstellen, den Grad der Bedrohung, lauernd über Motorisierung.
In vielen Großstädten auf der ganzen Welt ist sehr akutes Problem des städtischen Verkehrs. Verkehrsströme werden zusammen mit dem Wachstum der Städte durch natürliche wachsende, nicht unterordnen rationale Planung Platzierung von Wohn- und Industriegebiete. Verteilungs vorstädtischen Lebensstil führt zu einer Erhöhung der Anzahl von Privatautos. Ihre Ströme, Überflutung des Straßennetzes (schon gar nicht für sie bestimmt sind), was das Reisen rund um die Stadt während der Stunden der "peak" quälend langsam.In Japan, aufgrund der geringen Größe des Gebiets pro Flächeneinheit 5 mal mehr Autos als in den Vereinigten Staaten. Als Ergebnis der Konzentration des einen kritischen Wert erreicht hat. Die Lotse Verkehr im Zentrum von Tokio sind in Sauerstoffmasken arbeiten, ersetzt alle 2 Stunden und getestet "Intensivstation" in einer speziellen Box, wo saubere Luft gepumpt wird.

4,8(54 оценок)

Это интересно:

04.05.2023

Как выглядеть как Ария Монтгомери...

Компьютеры-и-электроника

17.02.2021

Как начать читать и писать на Leet: история, основы и особенности языка...

Хобби-и-рукоделие

19.01.2023

Как сделать клубнику оригами: подробный гайд с шаг за шагом...

Мир-работы

18.12.2022