1. Найдем производную функции у(х) y' = 4x - 4x^3; 2. Найдем значения х, при которых у'(х) = 0. Решим уравнение. 4х - 4х^3 = 0; 4х(1 - х^2) = 0; 4х(1 - х)(1 + х) = 0; Уравнение имеет 3 корня х = 0, х = 1, х = -1; 3. Функция у(х) имеет 3 точки экстремума: х = 0, х = 1, х = -1. Определим, какие из этих точек являются точками максимума, а какие точками минимума. Для этого найдем вторую производную функции у(х). у'' = 4 - 12x^2 = 4(1-3x^2); у''(0) = 4 * 1 = 4 > 0; х = 0 - точка минимума. y''(1) = y''(-1) = -8 < 0; х = 1 и х = -1 - точки максимума. ответ. 3 точки экстремума. Одна точка максимума х = 0; две точки минимума х = -1 и х = 1.
Пошаговое объяснение:
Пошаговое объяснение:
1) Берешь любые числа, которые подходят, чтобы при х-y = 8
это может быть, как я взяла х = 10, y = 2, может x = 9, тогда y = 1
и доп уравнение было бы x+y= 10
2) Оба уравнения должны быть одинаковыми, тогда и решение у них будет любое
потому что , если сократить 2х-2y = 16
2(x-y) = 16
x-y = 8, как и в условии
т.е ещё варианты: 3x-3y=24, 4x-4y=32 и т.д.
3) система не имеет решений тогда, когда два одинаковых уравнения равны разным числам
т.е. x-y = можно написать любое понравившееся число
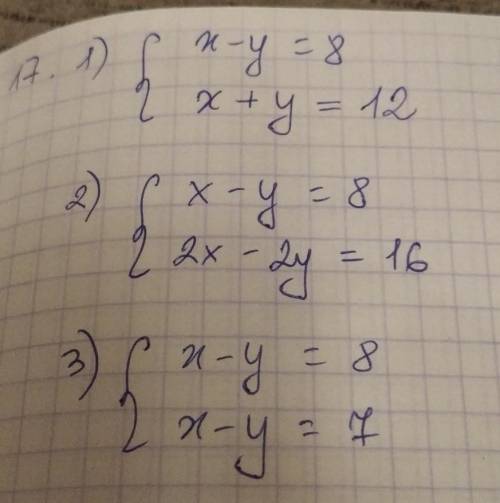
Пошаговое объяснение:
1)20×23=460м
2)920-460=460м
3)460÷20=23м/с
ответ 23м/с