3 число=9,6
2 число=9,6*1,5=14,4
1 число=9,6*2,5=24
Пошаговое объяснение:
Обозначаем третье число как х,выходя с данных задачи:
1 число=2,5х
2 число=1,5х
3 число=х
Составляем уравнение среднего арифметического трёх чисел:
(2,5х+1,5х+х)/3=16
5х/3=16
5х=48
х=9,6
Тоесть:
3 число=9,6
2 число=9,6*1,5=14,4
1 число=9,6*2,5=24
Немного теории.
Бесконечная периодическая десятичная дробь равна обыкновенной дроби, в числителе которой разность между всем числом после запятой и числом после запятой до периода. А знаменатель состоит из "девяток" (9) и "нулей" (0), причём "девяток" столько, сколько цифр в периоде, а "нулей" столько, сколько цифр до периода после запятой.
Теперь будем решать:
1)
0,(3)
Числитель: 3-0=3.
Знаменатель: 9 ("нулей" нет). ⇒
0,(3)=3/9=1/3.
2)
0,(1)
Числитель: 1-0=1.
Знаменатель: 9 ("нулей нет). ⇒
0,(1)=1/9.
3)
0,8(3)
Числитель: 83-8=75.
Знаменатель: 90. ⇒
0,8(3)=75/90=5/6.
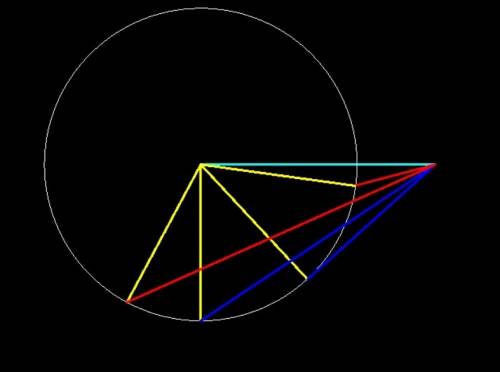
Пояснение к рисунку. Голубым цветом построен отрезок длиной 9, окружность - множество возможных положений конца отрезка длиной 6. Желтым - некоторые варианты положения отрезка длиной 6 (зеркальные не рассматриваем, чтобы не загромождать рисунок). Красным - значения а, когда треугольник становится тупоугольным (в случае малого а, тупым является угол между 6 и а, в случае большого - угол между 9 и 6). Синим цветом отрисованы граничные положения (значения а), когда
1) а становится катетом. При этом a = √9^2 - 6^2 = √81-36 = √45 = 3√5
2) а становится гипотенузой. При этом а = √9^2 + 6^2 = √81+36 = √117 = 3√13
При а между этими 2 значениями треугольник является остроугольным
3√5 < a < 3√13
16×3=48
х+1,5х+2,5х=5х
48:5=9,6 это третье число
9,6×1,5=14,4 это второе число
9,6×2,5=24 это третье число