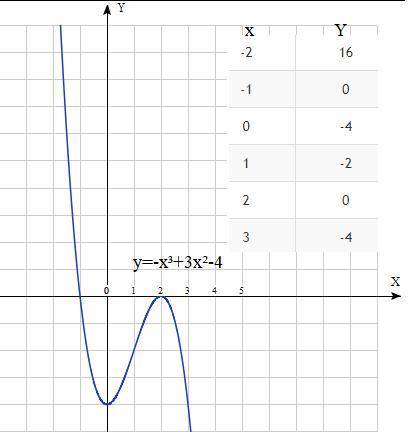
Постройте график функции y=-x³+3x²-4
Объяснение:
1) Область определения :D(y)=R ;
2)Четность-нечетность
у(-х)= -(-х)³+3*(-х)²-4=х³+3х²-4= -( -х³-3х²+4)≠у(х) общего вида;
3) а)Точки пересечения с осью ох( у=0)
-x³+3x²-4=0 , х=-1 , х=2
б)Точки пересечения с оу ( х=0)
y(0)=-0³+3*0²-4= -4 Точка (0; -4).
4)
а)стационарные точки у'= -3х²+6х
-3х²+6х=0 , -3х(х-2)=0 ,
х1=0, х2=2
б)Интервалы возрастания и убывания функции .
Если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X, т.е. у'>0.
-3х(х-2)>0
- - - - - (0)+ + + + +(2) - - - - - , х∈ (0;2) .
Т.к. функция определена и непрерывна при любом х, то можно включит концы отрезка х∈ [0;2] .
Если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X, т.е. у'<0.
Используя схему выше ⇒ х∈х∈(-∞; 0] и [2;+∞)
в)Экстремумы.
Точка х₀-точка максимума , если производная меняет свой знак с +на -.
Точка х₀- точка минимума , если производная меняет свой знак с - на +.
у' - + -
-----------------------(0)---------------------------(2)---------------
у убыв min возраст max убыв
х=2 точка максимума , у(2)= -(2)³+3*(2)-4= -8+6-4= -6.
х=0 точка минимума , у(2)=-0+0-4=-4
5) дополнительные точки
на графике
→ Если уменьшаемое увеличить на какое-либо число, то и разность увеличится на это же число.
→ Если уменьшаемое уменьшить на какое-либо число, то и разность уменьшится на это же число.
→ Если вычитаемое увеличить на какое-либо число, то разность уменьшится на это же число.
→ Если вычитаемое уменьшить на какое-либо число, то разность увеличится на это же число.
уменьшаемое - вычитаемое = разность
1. Как изменится разность, если уменьшаемое увеличить на 8?
· Если уменьшаемое увеличить на 8, то и разность увеличится на 8.
ответ: увеличится на 8
2. Как изменится разность, если уменьшаемое уменьшить на 4?
· Если уменьшаемое уменьшить на 4, то и разность уменьшится на 4.
ответ: уменьшится на 4
3. Как изменится разность, если вычитаемое увеличить на 7?
· Если вычитаемое увеличить на 7, то разность уменьшится на 7.
ответ: уменьшится на 7
4. Как изменится разность, если вычитаемое уменьшить на 5?
· Если вычитаемое уменьшить на 5, то разность увеличится на 5.
ответ: увеличится на 5
5. Как изменится разность, если уменьшаемое увеличить на 10, а вычитаемое на 6?
· Если уменьшаемое увеличить на 10, то и разность увеличится на 10.
· Если вычитаемое увеличить на 6, то разность уменьшится на 6.
10 - 6 = 4 ⇒ разность увеличится на 4
ответ: увеличится на 4
6. Как изменится разность, если уменьшаемое увеличить на 9, а вычитаемое на 12?
· Если уменьшаемое увеличить на 9, то и разность увеличится на 9.
· Если вычитаемое увеличить на 12, то разность уменьшится на 12.
12 - 9 = 3 ⇒ разность уменьшится на 3
ответ: уменьшится на 3
7. Как изменится разность, если уменьшаемое уменьшить на 14, а вычитаемое на 9?
· Если уменьшаемое уменьшить на 14, то и разность уменьшится на 14.
· Если вычитаемое уменьшить на 9, то разность увеличится на 9.
14 - 9 = 5 ⇒ разность уменьшится на 5
ответ: уменьшится на 5
8. Как изменится разность, если уменьшаемое уменьшить на 7, а вычитаемое на 11?
· Если уменьшаемое уменьшить на 7, то и разность уменьшится на 7.
· Если вычитаемое уменьшить на 11, то разность увеличится на 11.
11 - 7 = 4 ⇒ разность увеличится на 4
ответ: увеличится на 4
9. Как изменится разность, если уменьшаемое увеличить на 16, а вычитаемое уменьшить на 8?
· Если уменьшаемое увеличить на 16, то и разность увеличится на 16.
· Если вычитаемое уменьшить на 8, то разность увеличится на 8.
16 + 8 = 24 ⇒ разность увеличится на 24
ответ: увеличится на 24
10. Как изменится разность, если уменьшаемое увеличить на 3, а вычитаемое уменьшить на 6?
· Если уменьшаемое увеличить на 3, то и разность увеличится на 3.
· Если вычитаемое уменьшить на 6, то разность увеличится на 6.
3 + 6 = 9 ⇒ разность увеличится на 9
ответ: увеличится на 9
11. Как изменится разность, если уменьшаемое уменьшить на 20, а вычитаемое увеличить на 15?
· Если уменьшаемое уменьшить на 20, то и разность уменьшится на 20.
· Если вычитаемое увеличить на 15, то разность уменьшится на 15.
20 + 15 = 35 ⇒ разность уменьшится на 35
ответ: уменьшится на 35
12. Как изменится разность, если уменьшаемое уменьшить на 10, а вычитаемое увеличить на 30?
· Если уменьшаемое уменьшить на 10, то и разность уменьшится на 10.
· Если вычитаемое увеличить на 30, то разность уменьшится на 30.
10 + 30 = 40 ⇒ разность уменьшится на 40
ответ: уменьшится на 40
Пошаговое объяснение:
1) 2<|х+1|<5
Для |x+1|>2 допустим |x+1|=2
При x+1≥0: x+1=2; x₁=2-1=1
При x+1<0: -x-1=2; x₂=-2-1=-3
Проверка при x₁>1: |2+1|>2; |3|>2; 3>2; при x₂>-3: |-2+1|>2; |-1|>2; 1<2 - неравенство не выполняется.
Проверка при x₂<-3: |-4+1|>2; |-3|>2; 3>2 (если x₁>1) - неравенство выполняется.
Следовательно для |x+1|>2: -3>x>1
Для |x+1|<5 допустим |x+1|=5
При x+1≥0: x+1=5; x₁=5-1=4
При x+1<0: -x-1=5; x₂=-5-1=-6
Проверка при x₁>4: |5+1|<5; |6|<5; 6>5 - неравенство не выполняется.
Проверка при x₁<4: |3+1|<5; |4|<5; 4<5; при x₂>-6: |3+1|<5; |4|<5; 4<5 - неравенство выполняется.
Следовательно для |x+1|<5: -6<x<4
ответ: -6<x<-3∨1<x<4⇒x∈(-6; -3)∪(1; 4).
2) 1,7<|3-х|<4
Для |3-x|>1,7 допустим |3-x|=1,7
При 3-x≥0: 3-x=1,7; x₁=3-1,7=1,3
При 3-x<0: x-3=1,7; x₂=1,7+3=4,7
Проверка при x₁>1,3: |3-2|>1,7; |1|>1,7; 1<1,7 - неравенство не выполняется.
Проверка при x₁<1,3: |3-1|>1,7; |2|>1,7; 2>1,7; при x₂>4,7: |3-5|>1,7; |-2|>1,7; 2>1,7 - неравенство выполняется.
Следовательно для |3-x|>1,7: 1,3>x>4,7
Для |3-x|<4 допустим |3-x|=4
При 3-x≥0: 3-x=4; x₁=3-4=-1
При 3-x<0: x-3=4; x₂=4+3=7
Проверка при x₁>-1: |3-0|<4; |3|<4; 3<4; при x₂>7: |3-8|<4; |-5|<4; 5>4 - неравенство не выполняется.
Проверка при x₂<7: |3-0|<4; |3|<4; 3<4 (если x₁>-1) - неравенство выполняется.
Следовательно для |3-x|<4: -1<x<7
ответ: -1<x<1,3∨4,7<x<7⇒x∈(-1; 1,3)∪(4,7; 7).
3) 2,3<|х-4|<6
Для |x-4|>2,3 допустим |x-4|=2,3
При x-4≥0: x-4=2,3; x₁=2,3+4=6,3
При x-4<0: 4-x=2,3; x₂=4-2,3=1,7
Проверка при x₁>6,3: |7-4|>2,3; |3|>2,3; 3>2,3; при x₂>1,7: |2-4|>2,3; |-2|>2,3; 2<2,3 - неравенство не выполняется.
Проверка при x₂<1,7: |1-4|>2,3; |-3|>2,3; 3>2,3 (если x₁>6,3) - неравенство выполняется.
Следовательно для |x-4|>2,3: 1,7>x>6,3
Для |x-4|<6 допустим |x-4|=6
При x-4≥0: x-4=6; x₁=6+4=10
При x-4<0: 4-x=6; x₂=4-6=-2
Проверка при x₁>10: |11-4|<6; |7|<6; 7>6 - неравенство не выполняется.
Проверка при x₁<10: |9-4|<6; |5|<6; 5<6; при x₂>-2: |9-4|<6; |5|<6; 5<6 - неравенство выполняется.
Следовательно для |x-4|<6: -2<x<10
ответ: -2<x<1,7∨6,3<x<10⇒x∈(-2; 1,7)∪(6,3; 10).
4) 1,6<|х-1|<3
Для |x-1|>1,6 допустим |x-1|=1,6
При x-1≥0: x-1=1,6; x₁=1,6+1=2,6
При x-1<0: 1-x=1,6; x₂=1-1,6=-0,6
Проверка при x₁>2,6: |3-1|>1,6; |2|>1,6; 2>1,6; при x₂>-0,6: |0-1|>1,6; |-1|>1,6; 1<1,6 - неравенство не выполняется.
Проверка при x₂<-0,6: |-1-1|>1,6; |-2|>1,6; 2>1,6 (если x₁>2,6) - неравенство выполняется.
Следовательно для |x-1|>1,6: -0,6>x>2,6
Для |x-1|<3 допустим |x-1|=3
При x-1≥0: x-1=3; x₁=3+1=4
При x-1<0: 1-x=3; x₂=1-3=-2
Проверка при x₁>4: |5-1|<3; |4|<3; 4>3 - неравенство не выполняется.
Проверка при x₁<4: |3-1|<3; |2|<3; 2<3; при x₂>-2: |3-1|<3; |2|<3; 2<3 - неравенство выполняется.
Следовательно для |x-1|<3: -2<x<4
ответ: -2<x<-0,6∨2,6<x<4⇒x∈(-2; -0,6)∪(2,6; 4).
5) 4,5<|х+3|<7
Для |x+3|>4,5 допустим |x+3|=4,5
При x+3≥0: x+3=4,5; x₁=4,5-3=1,5
При x+3<0: -x-3=4,5; x₂=-4,5-3=-7,5
Проверка при x₁>1,5: |2+3|>4,5; |5|>4,5; 5>4,5; при x₂>-7,5: |-7+3|>4,5; |-4|>4,5; 4<4,5 - неравенство не выполняется.
Проверка при x₂<-7,5: |-8+3|>4,5; |-5|>4,5; 5>4,5 (если x₁>1,5) - неравенство выполняется.
Следовательно для |x+3|>4,5: -7,5>x>1,5
Для |x+3|<7 допустим |x+3|=7
При x+3≥0: x+3=7; x₁=7-3=4
При x+3<0: -x-3=7; x₂=-7-3=-10
Проверка при x₁>4: |5+3|<7; |8|<7; 8>7 - неравенство не выполняется.
Проверка при x₁<4: |3+3|<7; |6|<7; 6<7; при x₂>-10: |3+3|<7; |6|<7; 6<7 - неравенство выполняется.
Следовательно для |x+3|<7: -10<x<4
ответ: -10<x<-7,5∨1,5<x<4⇒x∈(-10; -7,5)∪(1,5; 4).
6) 3,2<|х+2|<6
Для |x+2|>3,2 допустим |x+2|=3,2
При x+2≥0: x+2=3,2; x₁=3,2-2=1,2
При x+2<0: -x-2=3,2; x₂=-3,2-2=-5,2
Проверка при x₁>1,2: |2+2|>3,2; |4|>3,2; 4>3,2; при x₂>-5,2: |-5+2|>3,2; |-3|>3,2; 3<3,2 - неравенство не выполняется.
Проверка при x₂<-5,2: |-6+2|>3,2; |-4|>3,2; 4>3,2 (если x₁>1,2) - неравенство выполняется.
Следовательно для |x+2|>3,2: -5,2>x>1,2
Для |x+2|<6 допустим |x+2|=6
При x+2≥0: x+2=6; x₁=6-2=4
При x+2<0: -x-2=6; x₂= -6-2=-8
Проверка при x₁>4: |5+2|<6; |7|<6; 7>6 - неравенство не выполняется.
Проверка при x₁<4: |3+2|<6; |5|<6; 5<6; при x₂>-8: |3+2|<6; |5|<6; 5<6 - неравенство выполняется.
Следовательно для |x+2|<6: -8<x<4
ответ: -8<x<-5,2∨1,2<x<4⇒x∈(-8; -5)∪(1,2; 4)