360 тысяч
Пошаговое объяснение:
За год надо платить:
5 тысяч*12=60 тысяч
Так как лет:
60 тысяч*6=360 тысяч
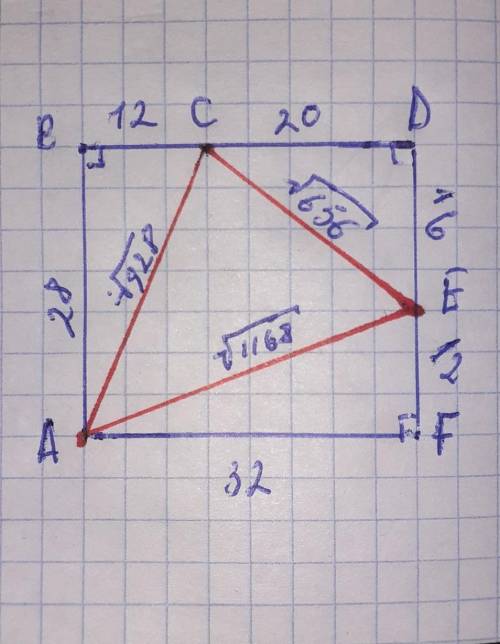
площадь S=376м²
1 клетка 4м
стороны треугольника находим через теорему Пифагора .
треугольник вписан в прямоугольник из клеток с размером в длину 8 и ширину 7 клеток.
треугольник ΔACE вписанный в четырёхугольный прямоугольник □ ABDF , образует прямоугольные треугольники ΔABC где<В=90° , ΔCDE где <D=90° и
ΔAFE где <F=90°.
AF=BC+CD ,
AB=DE+EF ,
BC=3 кл ,
CD=5 кл ,
AF=8 кл ,
DE=4 кл ,
EF=3 кл ,
AB=7 кл.
переводим на метры
BC=3×4=12м,
CD=5×4=20м,
AF=8×4=32м,
DE=4×4=16м,
EF=3×4=12м ,
AB=7×4=28м .
по теореме Пифагора находим для каждого прямоугольного треугольника гипотенузы, которые являются в свою очередь сторонами ΔACE.
для ΔABC
AC=√AB²+BC²=√28²+12²=√784+144=√928
для ΔCDE
CE=√CD²+DE²=√20²+16²=√400+256=√656
для ΔAFE
AE=√AF²+EF²=√32²+12²=√1024+144=√1168
находим площадь прямоугольных треугольников
ΔABC
S1=ab/2= AB×BC/2=28×12/2=168 м²
ΔCDE
S2=CD×DE/2=20×16/2=160 м²
ΔAFE
S3= AF×EF/2=32×12/2=192 м²
площадь четырёхугольника □ABDF
S□=a×b=AB×AF=28×32=896 м²
площадь четырехугольника равна сумме площадей треугольников ΔACE, ΔABC , ΔCDE и ΔAFE:
S□=SΔACE +S1+S2+S3 ,
отсюда можно найти площадь ΔACE
SΔACE= S□- (S1+S2+S3),
SΔACE=896 - (168 + 160 + 192)=896 - 520 = 376м²
периметр участка, треугольника ΔACE
P=AC+CE+AE=√928 +√656 +√1168 = округленно 90,25 м
Старший Знаток
1) y=log_5(4-2x-x^2)+3
Область определения:
4 - 2x - x^2 > 0
x^2 + 2x - 4 < 0
x^2 + 2x + 1 - 5 < 0
(x+1)^2 - (√5)^2 < 0
(x+1-√5)(x+1+√5) < 0
x ∈ (-1-√5; -1+√5)
Локальные экстремумы будут в точках, в которых производная равна 0.
Производная
y'= \frac{-2-2x}{(4-2x-x^2)*ln(5)} = \frac{-2(x+1)}{(4-2x-x^2)*ln(5)} =0
x = -1 ∈ (-1-√5; -1+√5)
y(-1)=log_5(4-(-2)-(-1)^2)+3=log_5(4+2-1)+3=1+3=4
Знаменатель > 0, потому что скобка (4-2x-x^2) > 0, по области определения логарифма. Числитель -2(x+1)>0 при x<-1, значит, график возрастает, а при x>-1 график убывает. Значит, -1 точка максимума.
ответ: Наибольшее значение y(-1) = 4
2) y=log_3(x^2-6x+10)+2
Область определения:
x^2 - 6x + 10 > 0
x^2 - 6x + 9 + 1 > 0
(x - 3)^2 + 1 > 0
Сумма квадрата и положительного числа положительна при любом x.
x ∈(-oo; +oo)
Локальные экстремумы будут в точках, в которых производная равна 0.
y' = \frac{2x-6}{(x^2-6x+10)*ln(3)} = \frac{2(x-3)}{(x^2-6x+10)*ln(3)} =0
x = 3
y(3)=log_3(9-6*3+10)+2=log_3(9-18+10)+2=0+2=2
Здесь все наоборот. Знаменатель тоже >0. Числитель 2(x-3)<0 при x<3 (график убывает) и 2(x-3)>0 при x>3 (график возрастает).
Значит, 3 - точка минимума.
ответ: Наименьшее значение y(3) = 2
Пошаговое объяснение:
в году 12 мес. 12×5000=60'000₽ в год
60'000×6=360'000₽ за 6 лет