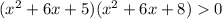
Метод интервалов.
Приравняем неравенство к нулю и найдем нули множителей:

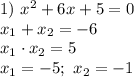
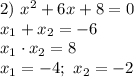
Перепишем многочлены вида 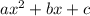 на множители вида
на множители вида 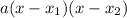 , где
, где 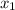 и
и 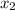 — корни квадратного уравнения
— корни квадратного уравнения 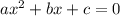
Имеем:
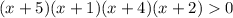
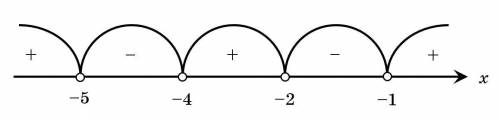
Начертим координатную прямую и отметим выколотыми точками (так как неравенство строгое) нули множителей, и определим знак на каждом интервале ("+", если на этом интервале функция 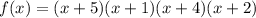 выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.
выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.
Следовательно, промежутками, на которых функция 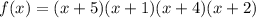 больше нуля (выше оси абсцисс), являются:
больше нуля (выше оси абсцисс), являются:
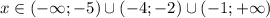
Неравенство вида 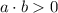 выполняется в двух случаях:
выполняется в двух случаях:
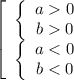
Следовательно, рассмотрим первый случай:
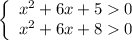
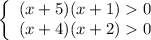
Здесь  и
и 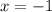 — точки пересечения графика функции
— точки пересечения графика функции 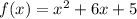 с осью абсцисс, и
с осью абсцисс, и 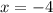 и
и  — точки пересечения графика функции
— точки пересечения графика функции 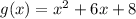 с осью абсцисс.
с осью абсцисс.
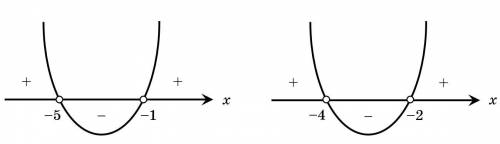
Изобразим две параболы для каждого неравенства и определим те абсциссы, при которых каждая из них больше нуля (см. вложение). Имеем промежутки:
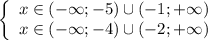
Следовательно, промежутками, при которых оба неравенства выполняются одновременно, являются:
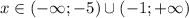
Рассмотрим второй случай:
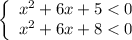
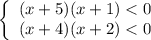
Из тех же парабол определим те абсциссы, при которых каждая из них меньше нуля:
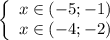
Следовательно, промежутком, при котором оба неравенства выполняются одновременно, является:
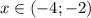
Объединим оба случая и получим решение неравенства:
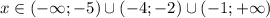
ответ: 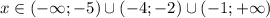
Пошаговое объяснение:
средняя скорость - весь путь на общее затраченное время
V = S/T формула (1)
обший путь S = S₁ +S₂ (т.е две поовины)
для каждой найдем время и скорость
первую половину пути лодка шла v₁=12 км/час за t часов S₁=12t
вторую половину со скоростью v₂ = 4 км/час, т.е. в 3 раза медленнее, значит времени она затратила в 3 раза больше т.е. 3t часов S₂=4*3t
теперь можем найти весь путь и всё время
весь путь
S =(12*t) + (4*3t) =24t
всё время Т = t + 3t = 4t
это подставляем в формулу (1) и получаем среднюю скорость
V = 24t / 4t = 6 (км/час)
ответ
средняя скорость 6 км/час
4.7 тыс. ответов
4.1 млн пользователей, получивших
Пусть Х км/ч - скорость 1-го бегуна ,
тогда (Х +5) - скорость 2-го бегуна
20 мин = 20/60=1/3 ч - время 1-го бегуна
20 мин - 5 мин =15 мин =15/60=1/4 ч - время 2-го бегуна
1/3 Х - путь 1-го бегуна
1/4(Х+5) - путь 2-го бегуна
Известно, что путь 1-го бегуна меньше на 1/3 км
Составим уравнение:
1/4( Х+5 км ) -1/3 Х = 1/3 км
1/4 Х + 5/4 км - 1/3 Х =1/3 км
- 1/12 Х = - 5/4 км +1/3 км
1/12 Х = 11/12 км
Х= 11/12 : 1/12
Х= 11 км /ч - скорость 1-го бегуна
(Х+5)= 11*5= 16 км/ч - скорость 2-го бегуна
ax^2 + bx + c = 0
D = b^2 - 4ac
x12 = (-b +- √D)/2a
(x^2+6x+5)*(x^2+6x+8)>0
раскладываем многочлены
(x^2+6x+5) = (x + 5)(x + 1)
D = 36 - 20 = 16
x12=(-6 +- 4)/2 = -5 -1
(x^2+6x+8) = (x + 2)(x + 4)
D = 36 - 32 = 4
x12 = (-6 +- 2)/2 = -4 -2
(x + 5)(x + 1)(x + 2)(x + 4) > 0
применяем метод интервалов
(-5) (-4) (-2) (-1)
x∈(-∞, -5) U (-4, -2) U (-1, +∞)