2м\ч
Пошаговое объяснение:
х-скорость теч реки
15,4-х=11,4+х
х+х=15,4-11,4
2х=4
х=2км\ч скор теч реки
) 
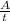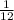частей/год. Тогда второй выполняет тот же объем работ за 8 лет (A=1; t=8; 
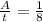) и третий за "x" лет (A=1; t=x; 
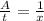). Из условия известно, что три насоса вместе справляются с работой за 4 года (A=1; t=4; 
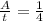). Значит общая производительность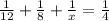
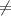0 ⇒ можем обе части уравнения умножить на одно и то же число (24x).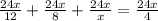
2х = 28,6; х = 14,3 км/ч;
Пошаговое объяснение:
1. Принимаем за х скорость моторки без учета течения реки, за у скорость потока воды в реке.
2. Составим два уравнения:
х - у = 13;
х + у = 15,6;
3. Складывая эти уравнения, получим одно уравнение с одним неизвестным:
2х = 28,6; х = 14,3 км/ч;
ответ: скорость моторки без учета течения реки 14,3 км/ч.