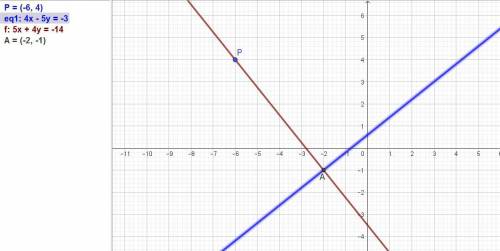
Дана точка Р(-6;4) и прямая 4x-5y+3=0 в общем виде Ax + By + C =0.
У прямой, перпендикулярной к заданной прямой, коэффициенты А и В меняются на (-В) и А.
Получаем 5x + 4y + C = 0. Так как этот перпендикуляр должен проходить через точку Р(-6; 4), то подставим координаты Р в уравнение.
5*(-6) + 4*4 + С =0, отсюда С = 30 - 16 = 14.
Уравнение 5x + 4y + 14 = 0.
Проекция точки Р на заданную прямую - это точка пересечения прямой и перпендикуляра. Находим координаты точки пересечения, решая систему:
{4x - 5y + 3 = 0, умножим на (-5) = -20x + 25y - 15 = 0
{5x + 4y + 14 = 0. умножим на 4 = 20x + 16y + 56 = 0
41 y + 41 = 0,
y = -41/41 = -1, x = (5*y - 3) /4 = (5*(-1)) - 3)/4 = -8/4 = -2.
ответ: проекция точки Р на прямую 4х-5у+3=0
имеет координаты (-2; -1).
Они равны. Знак =