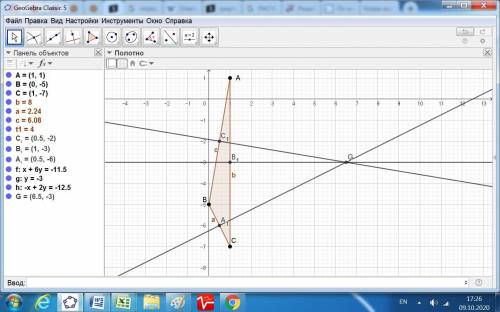
Даны вершины треугольника: A(1; 1), B(0; -5), C(1; -7).
Находим координаты двух середин сторон.
А1 = (1/2)ВС = (0,5; -6).
В1 = (1/2)АС = (1; -3).
Определяем уравнения сторон:
ВС: вектор ВС = (1; -2),
каноническое уравнение (х/1) = ((у + 5)-(-2)),
с угловым коэффициентом у = -2х - 5.
Уравнение перпендикуляра к = -1/к(ВС) = -1/(-2) = 1/2.
Уравнение имеет вид у = (1/2)х + в, подставим координаты точки А1:
-6 = (1/2)*0,5 + в, отсюда в = -6 -0,25 = -6,25.
Уравнение перпендикуляра через А1: у = (1/2)х - 6,25.
Так как координаты точек А и С по оси Ох равны, то эта сторона вертикальна, поэтому срединный перпендикуляр к ней - горизонтальная линия, проходящая через точку В1(1; -3).
Уравнение через В1: у = -3.
Находим координаты точек пересечения срединных перпендикуляров: приравниваем уравнения (1/2)х - 6,25 = -3
Отсюда х = (-3 + 6,25)*2 = 3,25*2 = 6,5.
ответ: точка пересечения перпендикуляров G(6,5; -3).
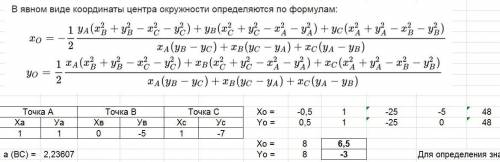
Есть общая формула вычисления точки пересечения срединных перпендикуляров треугольника по координатам вершин.
Она дана во вложении.
Дано:
L₁ = 2.2 м = расстояние, которое проходит переднее колесо за 1 оборот
L₂ = 3.4 м = расстояние, которое проходит заднее колесо за 1 оборот
ΔN = 150 оборотов - разница между числом оборотов переднего и заднего колёс.
Найти:
s - расстояние, которое проходит тележка
N₁ = s : L₁ - число оборотов, которое сделало переднее колесо на расстоянии s
N₂ = s : L₂ - число оборотов, которое сделало заднее колесо на расстоянии s
По условию
ΔN = N₁ - N₂
ΔN = s : L₁ - s : L₂
s = ΔN · L₁ · L₂ : ( L₂ - L₁)
Подставим данные
s = 150 · 2.2 · 3.4 : (3.4 - 2.2)
s = 935 (м)
Тележка м
а)-2;-1;0;1;2;3;3;4;5.
б)-10;-9;-8;-7;-6;-5;-4;-3;-2;-1;0;1;2;3;4;5;6.
в) 0.