Прямокутник одна із сторін дорівнює 7 см а діагональ 25 см об’являть об’єм утвореного тіла обертання

👇

Открыть все ответы

Ответ:

ronaldopenzap016aa

22.02.2020

ответ: числа 12, 24, 36, 48.
Решение :
1 дес. + (1*2) ед. = 1 дес. 2 ед. =12
2 дес. + (2*2) ед.= 2 дес. 4 ед. = 24
3 дес.+ (3*2) ед.= 3 дес. 6 ед. = 36
4 дес. + (4*2) ед. = 4 дес. 8 ед. =48
Далее идут не подходящие числа , т.к. число единиц, умноженное на 2 , больше десятка :
5 дес + (5*2) = 5 дес. + 10 ед = 6 дес. = 60 - не подходит
6 дес. + (6*2) ед. = 6 дес. + 12 ед. = 72 - не подходит
7 дес. + (7*2) ед. = 7 дес. + 14 ед.= 84 - не подходит
8 дес. + (8*2) ед= 8 дес. + 16 ед. = 96 - не подходит

4,4(30 оценок)

Ответ:

viktoriya2000ok

22.02.2020

Будем разбивать на несколько случаев.

1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 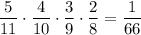$\dfrac{5}{11}\cdot \dfrac{4}{10}\cdot \dfrac{3}{9}\cdot\dfrac{2}{8}=\dfrac{1}{66}$ . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна $\dfrac{3}{12}\cdot\dfrac{2}{11}\cdot\dfrac{1}{10}=\dfrac{1}{220}$ . 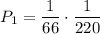По теореме умножения $P_1=\dfrac{1}{66}\cdot\dfrac{1}{220}$

2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 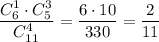$\dfrac{C^1_6\cdot C^3_5}{C^4_{11}}=\dfrac{6\cdot10}{330}=\dfrac{2}{11}$ . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 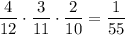$\dfrac{4}{12}\cdot\dfrac{3}{11}\cdot\dfrac{2}{10}=\dfrac{1}{55}$ . По теореме умножения: $P_2=\dfrac{2}{11}\cdot\dfrac{1}{55}$

3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 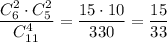$\dfrac{C^2_6\cdot C^2_5}{C^4_{11}}=\dfrac{15\cdot10}{330}=\dfrac{15}{33}$ . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 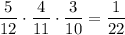$\dfrac{5}{12}\cdot\dfrac{4}{11}\cdot\dfrac{3}{10}=\dfrac{1}{22}$ . По теореме умножения : $P_3=\dfrac{15}{33}\cdot\dfrac{1}{22}$

4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна $\dfrac{C^3_6\cdot C^1_5}{C^4_{11}}=\dfrac{20\cdot5}{330}=\dfrac{10}{33}$ . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна $\dfrac{6}{12}\cdot\dfrac{5}{11}\cdot\dfrac{4}{10}=\dfrac{1}{11}$ . 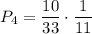По теореме умножения: $P_4=\dfrac{10}{33}\cdot\dfrac{1}{11}$

5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 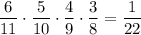$\dfrac{6}{11}\cdot\dfrac{5}{10}\cdot\dfrac{4}{9}\cdot\dfrac{3}{8}=\dfrac{1}{22}$ . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 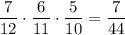$\dfrac{7}{12}\cdot\dfrac{6}{11}\cdot\dfrac{5}{10}=\dfrac{7}{44}$ . По теореме умножения: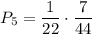 $P_5=\dfrac{1}{22}\cdot\dfrac{7}{44}$

Итого, по теореме сложения:

$P=P_1+P_2+P_3+P_4+P_5=\dfrac{1}{66}\cdot\dfrac{1}{220}+\dfrac{2}{11}\cdot\dfrac{1}{55}+\dfrac{15}{33}\cdot\dfrac{1}{22}+\\ \\ +\dfrac{10}{33}\cdot\dfrac{1}{11}+\dfrac{1}{22}\cdot\dfrac{7}{44}=\dfrac{427}{7260}\approx 0{,}0588$