Відповідь:
Покрокове пояснення:
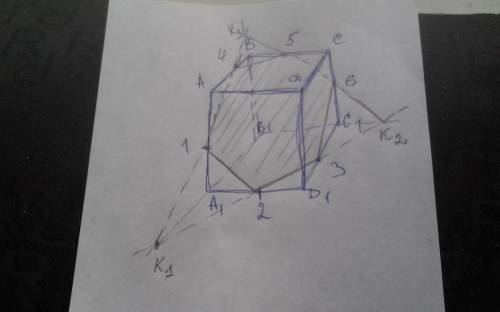
Точки можно соединять только если они находятся в одной плоскости, также и прямие, ищем пересечения на плоскости
1. К1- точка пересечения прямих 23 и А1В1
Соединяем К1 и точку 1, пересечение етой прямой с АВ дает точку 4
2. К3 - точка пересечения прямихиВВ1 и 14
К2- точка пересечения прямих 23 и В1С1
Точки К3 и К2 лежат в одной плоскостии ВСС1В1
Поетому пересечение прямих К2К3 и СС1 дает точку 6, а с пересечением ВС точку 5
3. Соединяем точки 123465 имеем наше пересечение
На второй фотографии: так как точки 1 и 2, 2 и 3, 3 и 1 лежат на соответствующих гранях, то их просто соединяют
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Дано:
а) ∠А1В1С1 - линейный угол двугранного угла АВВ1С,
т.к. данная фигура - куб.
б) Надо найти угол между плоскостями
∠ADB - линейный угол двугранного угла ADD1B;
в) Проведем B1K; проведем KE || AA1; проведем диагональ квадрата ВЕ. Требуется найти линейную меру двугранного угла между
плоскостями АА1В1В и KB1BE. А1В1 ⊥ ВВ1, B1K ⊥ ВВ1.
Таким образом, ∠А1В1K - линейный угол двугранного угла ABB1K.
Точку А симметрично отображаем относительно прямой y = x это будет точка В с координатами (3;2), затем точку В симметрично отобразим относительно прямой y = 1, получим
ответ: B'(3;0).