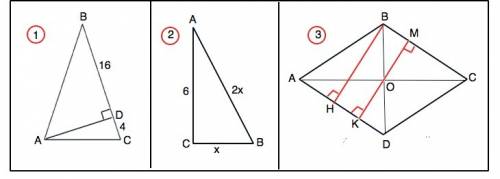
1) ВС=AD+CD=20 (см)
∆ АВС равнобедренный, АВ=ВС=20 (см)
∆ АВD- прямоугольный
AD=√(AB²-BD²)=√144=12 (см)
Из ∆ АDC гипотенуза АС=√(AD²+CD²)=√160=4√10 см
S (ABC)=AD•BC:2=12•20:2=120 см²
* * *
2) Примем меньший катет равным х, тогда гипотенуза 2х.
По т.Пифагора (2х)²-х*=36 ⇒ х=√12=2√3 м – это ответ.
* * *
3) Ромб - параллелограмм с равными сторонами, его диагонали взаимно перпендикулярны. Отрезок, перпендикулярный противоположным сторонам параллелограмма равен его высоте.
МК параллелен и равен высоте ромба ВН.
Точка О делит диагонали пополам, а сам ромб - на 4 равных прямоугольных треугольника.
АО=АС:2=32:2=16 .
ВО=ВD:2=12
Из ∆ АОВ по т.Пифагора АВ=√(АО²+ВО²)=√ 400=20
а) Площадь ромба равна половине произведения его диагоналей.
S=AC•BC:2=32•24:2=384
б) Площадь ромба равна произведению высоты на его сторону.
S=a•h – h=S:a
h=384:20=19,2 (ед. длины)
На конструкцию можно смотреть с 4 сторон: спереди, слева, сзади и справа. Просчитаем максимально возможное число кубиков в каждом случае, зная что максимальные количества кубиков в башнях по линиям соответственно равны 2, 4, 1, 3.
1. Смотрим спереди: соответствующие линии показаны на картинке. Максимальные количества башен по линиям соответственно равны 3, 1, 2, 3.
Итого: 2·3+4·1+1·2+3·3=6+4+2+9=21
2. Смотрим слева. Максимальные количества башен по линиям соответственно равны 2, 2, 2, 3.
Итого: 2·2+4·2+1·2+3·3=4+8+2+9=23
3. Смотрим сзади. Максимальные количества башен по линиям соответственно равны 3, 2, 1, 3.
Итого: 2·3+4·2+1·1+3·3=6+8+1+9=24
4. Смотрим справа. Максимальные количества башен по линиям соответственно равны 3, 2, 2, 2.
Итого: 2·3+4·2+1·2+3·2=6+8+2+6=22
Максимальное количество при взгляде сзади - 24.
ответ: 24