Задача. Фирма среди своих сотрудников разыгрывает новогоднюю лотерею. В лотерее 10 билетов, из которых 6 выигрышных. Сотрудник фирмы покупает 2 билета. Какова вероятность того, что у этого сотрудника выиграет хотя бы один билет? Результат округлите до сотых.
Количество возможных элементарных исходов равно числу вынуть два билета из 10 билетов, т.е. .
Подсчитаем количество благоприятных исходов. Для этого нужно определить сколькими этот сотрудник может выбрать хотя бы один выигрышный билет. Таких
Машины встретятся через 2 часа 30*2*2=120 (60км каждая) через 1ч 20 мин мотоцикл встретится с машиной(мот-80км,машины по 40км) у машин до встречи остается по 20 км это пол часа общее 40 км у мотоцикла за пол часа 30 км 40+60=100(общая скорость мот и маш) при растоянии 40 км 40/100=0.4 40*0,4=16 и 60*0,4=24(проедет мот до встречи со второй машиной)- ещё 24 минуты пути\остается 8км до встречи машин-это 6 мин,так как машина проезжает 1 км за 1,5минуты(2 навстречу за 2 км),а мот 1км за 1 мин (40+16)*2=112 и 8/2*1,5=6 мин осталось у машин у мотоцикла тоже осталось 6 минут проехать 6 км до места встречи машин и того 80+24+6=110 км проедет мотоцикл до встречи машин!
будем решать от противного(положного). этап 1. предположим что есть такие 2 числа. тогда при делении мы получим 2 или 3 потому что минимальное число 1234, а максимальное 4321 4321 : 1234 = 3,*** < 4 если при делении 1 - то числа равные (не может быть) этап 2. если при делении получим 2 тогда при умножении меньшего получим в составе большего цифры: 1*2 = 2, 2 * 2 = 4, 3 * 2 = 6 - чего быть не может. остается только вариант, когда одно в 3 раза меньше другого. этап 3. рассмотрим меньшее из чисел. если последнюю цифру поставить 2 или 3 то в результате умножения получим 6 или 8 - чего быть не может. если последняя цифра = 1 то первая 2, 3 или 4 умноженная на 3 даст больше 4 - противоречие к (если последняя цифра = 1) рассмотрим последний вариант, где последняя цифра = 4, первая соответственно = 1 (2 и 3 умноженные на 3 > 4) 4 * 3 = 12 если вторая цифра = 2 то 2*3 + 1 = 7 - противоречие если вторая цифра = 3 то 3 * 3 + 1 =10 (или 0) - опять противоречие.
таким образом мы исключили все варианты образования меньшего из чисел и тем самым показали что 2 чисел с указанными свойствами не существует.
Задача. Фирма среди своих сотрудников разыгрывает новогоднюю лотерею. В лотерее 10 билетов, из которых 6 выигрышных. Сотрудник фирмы покупает 2 билета. Какова вероятность того, что у этого сотрудника выиграет хотя бы один билет? Результат округлите до сотых.
Количество возможных элементарных исходов равно числу вынуть два билета из 10 билетов, т.е.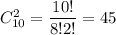 .
.
Подсчитаем количество благоприятных исходов. Для этого нужно определить сколькими этот сотрудник может выбрать хотя бы один выигрышный билет. Таких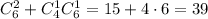
Искомая вероятность: