Для начала нужно решить соответствующее линейное однородное дифференциальное уравнение, выполнив замену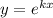 
.
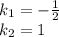
Общее решение однородного диф. уравнения: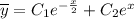 
.
Рассмотрим функцию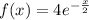 
. Здесь 
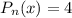, где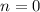 
, 
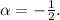Сравнивая 
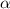с корнями характеристического уравнения и принимая во внимая, что
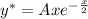
Определим первые две производные функции частного решения и подставляем в исходное дифференциальное уравнение одновременно разделив обе части на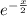 
.
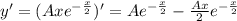
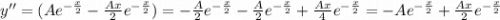
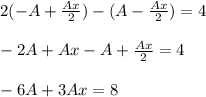
Приравниваем коэффициенты при степенях x
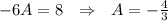
Общее решение линейного неоднородного дифференциального уравнения ищем как сумму общего однородного диф. уравнения и частного решения
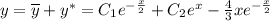
1) Три целых одна четвертая (целая часть - три целых, дробная часть - одна четвертая)
2) Восемь целых пять седьмых (целая часть - восемь целых, дробная часть - пять седьмых)
3) Семь целых одна двенадцатая (целая часть - 7 целых, дробная часть - одна двенадцатая)
4) Девять целых семь девятых (целая часть - 9 целых, дробная часть - семь девятых)
5) Сорок одна целая семь шестнадцатых (целая часть - 41 целая , дробная часть - семь шестнадцатых)
6) Восемьдесят одна целая тринадцать двадцать пятых (целая часть - 81 целая, дробная часть - тринадцать двадцать пятых)
Пошаговое объяснение: