-7x²+6x+1>0
-7x²+6x+1>0 | :(-1)
7x²-6x-1<0 (a=7; b=-6; c=-1)
Д: b² - 4ac = 6² - 4•7• (-1)= 36+28 = 64
√Д = √64 =8
X¹(только эта единица внизу) = -b+√Д: 2a (здесь дробовая чёрточка, просто здесь ставить хз как) =
6 +8
—— = 1
14
X² (тоже внизу) = -b +√Д:2а (также как в первом дробь) =
6-8
—— = -0, 14.
14
-0,14 <0
Вот и все решение. Там просто в формулы подставлять эти a,b,c которые записаны вверху в скобках. Там, где Д (дискриминант ) не - 6, а сразу 6 ибо в квадрате, а число в квадрате не может быть отрицательным. 36 + 28 ибо — умноженный на — получаем +.
Начнём считать с конца и посмотрим, как можно представить количество монет после действий какого-нибудь из пиратов:
Каждый пират забирал одну монету и 1/6 остатка. Пусть количество монет после действия пирата равно 5k, тогда до его действий монет было 6k + 1, при этом k - целое число. При этом 6k + 1 должно представляться в виде 5k (кроме, возможно, изначального количества монет).
Так как 5k ≡₅ 0 и 6k + 1 ≡₅ 0, то 6k ≡₅ -1, откуда k ≡₅ -1. Значит, 5k можно представить в виде 5ᵃ * k - 5. Посмотрим, сколько монет было одной операцией назад:
(5ᵃ * k - 5) : 5 * 6 + 1 = (5^(a-1) * k - 1) * 6 + 1 = 5^(a-1) * 6k - 5. Заметим, что "-5" сохраняется, а "a" уменьшается на 1. Пусть k не делится на 5 (иначе поделим k на 5 и увеличим a на 1), тогда k должно быть в конце (в начале при подсчёте с конца) наименьшим из возможных, значит, k должно быть равно 1. В начале a должно было быть наименьшим из возможных (в конце при подсчёте с конца), иначе можно было бы домножить k на 5, так как обратных операций больше не будет. Значит, в конце a = 6, а k = 1.
5⁶ * 1 - 5 = 15620.
ответ: 15620 монет.
P.S. Верность ответа проверена с программы на языке Python.
4/3 (1 1/3)
Пошаговое объяснение:
6x^2-11x+4=0
Квадратное уравнение, найдем корни с дискриминанта
D=b^2-4ac
D=121-4*6*4=121-96=25=5^2
x=(-b+-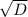 )/2a
)/2a
x=(11+5) / 12 = 16/12 = 4/3
x=(11-5)/12=1/2
Наибольший корень 4/3
ответ 4/3