У Кати было 4 набора карандашей по 12 шт. в каждом и 4 набора фломастеров по 8 шт. в каждом. Сколько всего карандашей и фломастеров у Кати?
12 * 4 + 8 * 4 = 48 + 32 = 80 шт. - всего
ответ: у Кати было всего 80 карандашей и фломастреров.
Брат нашёл 7 боровиков, а сестра 3 боровика. Сколько боровиков нашёл папа, если он собрал в 5 раз больше, чем его дети?
(7 + 3) * 5 = 50 боровиков - нашёл папа.
В 3х классах было по 23 ученика, а в 2х классах было по 11 учеников. Сколько было всего учеников?
23 * 3 + 11 * 2 = 69 + 22 = 91 уч. - всего.
a) x∈(-∞;-2]∪(-1;1)∪[7;+∞)
b) x∈(0;1]
c) x∈[0;π²/4]∪[(-π/2+2kπ)²; (π/2+2kπ)²], k∈N
Пошаговое объяснение:
a) y=arcsin[(5x+13)/(x²-1)]
x²-1≠0⇒x≠±1
-1≤(5x+13)/(x²-1)≤1
1) (5x+13)/(x²-1)≤1
1-(5x+13)/(x²-1)≥0
[(x²-1)-(5x+13)]/(x²-1)≥0
(x²-5x-14)/(x²-1)≥0⇔(x²-5x-14)·(x²-1)≥0, x≠±1
(x+2)(x+1)(x-1)(x-7)≥0
Решая методом интервалов, имеем
x∈(-∞;-2]∪(-1;1)∪[7;+∞)
b) y=arcsin√(1-x)+arccos√x+∛(x-1)+lnx
1) arcsin√(1-x) имеет смысл при 1-x≥0 ∩ √(1-x)≤1⇒x∈[0;1]
arccos√x имеет смысл при x≥0 ∩ √x≤1⇒x∈[0;1]
∛(x-1) имеет смысл при ∀x∈R
lnx имеет смысл при x>0⇒x∈(0;+∞)
[0;1]∩[0;1]∩R∩(0;+∞)=(0;1]
c)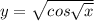
√x имеет смысл при x≥0
cost≥0⇒-π/2+2kπ≤t≤π/2+2kπ
-π/2+2kπ≤√x≤π/2+2kπ
при к отрицательном решения нет, так как 0≤√x
при к=0, 0≤√x≤π/2⇒0≤x≤(π/2)²⇒0≤x≤π²/4
при к≥1 -π/2+2kπ≤√x≤π/2+2kπ⇒(-π/2+2kπ)²≤x≤(π/2+2kπ)²
x∈[0;π²/4]∪[(-π/2+2kπ)²; (π/2+2kπ)²], k∈N
d)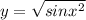
2kπ≤x²≤π+2kπ, k=0;1;2;3;4;...
при к=0, х²≤π=>-√π≤х≤√π
при к €N, решаем двойные неравенства вида 2kπ≤x²≤π+2kπ, которые по сути являются системой неравенств 2kπ≤x², x²≤π+2kπ. Решением их является пересечение множеств их решений