![\int \dfrac{dx}{sin^2x\cdot cos^4x}=\int \dfrac{1}{sin^2x}\cdot \dfrac{1}{cos^2x}\cdot \dfrac{dx}{cos^2x}=\int (1+ctg^2x)\cdot (1+tg^2x)\cdot \dfrac{dx}{cos^2x}=\\\\\\=\int \Big(1+\dfrac{1}{tg^2x}\Big)(1+tg^2x)\cdot d(tgx)=\Big[\; t=tgx\; \Big]=\int \dfrac{(1+t^2)^2}{t^2}\, dt=\\\\\\=\int \dfrac{1+2t^2+t^4}{t^2}\, dt=\int \Big(\dfrac{1}{t^2}+2+t^2}\Big)\, dt=-\dfrac{1}{t}+2t+\dfrac{t^3}{3}+C=\\\\\\=-\dfrac{1}{tgx}+2tgx+\dfrac{tg^3x}{3}+C](/tpl/images/1086/8395/04e49.png)
Периметр прямоугольника по формуле: Р = 2*(a+b).
Рисунок к задаче в приложении.
ДАНО: a = 4 м, b = 3 м, c = 3 м.
РЕШЕНИЕ
Из рисунка видно, что можно применить два варианта расчёта.
Вариант 1. Сумма периметров двух пар стен.
Р₁ = 2*(a+b) = 2*(4+3) = 14 м - периметр длинной стены.
Р₂ = 2*(b+c) = 2*(3+3) = 12 м - периметр короткой стены.
Р = 2*(Р₁+Р₂) = 2*(14+12) = 52 м - периметр стен - ОТВЕТ 1
Вариант 2. Сумма длин всех рёбер прямоугольника плюс 4 длины высоты стен.
Формула суммы длин рёбер параллелепипеда:
P₁ = 4*(a+b+c) = 4*(4+3+3) = 4*10 = 40 метров
Р = Р₁ + 4*b = 40 + 4*3 = 40+12 = 52 м - периметр - ОТВЕТ 2
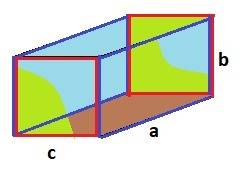
Периметр прямоугольника по формуле: Р = 2*(a+b).
Рисунок к задаче в приложении.
ДАНО: a = 4 м, b = 3 м, c = 3 м.
РЕШЕНИЕ
Из рисунка видно, что можно применить два варианта расчёта.
Вариант 1. Сумма периметров двух пар стен.
Р₁ = 2*(a+b) = 2*(4+3) = 14 м - периметр длинной стены.
Р₂ = 2*(b+c) = 2*(3+3) = 12 м - периметр короткой стены.
Р = 2*(Р₁+Р₂) = 2*(14+12) = 52 м - периметр стен - ОТВЕТ 1
Вариант 2. Сумма длин всех рёбер прямоугольника плюс 4 длины высоты стен.
Формула суммы длин рёбер параллелепипеда:
P₁ = 4*(a+b+c) = 4*(4+3+3) = 4*10 = 40 метров
Р = Р₁ + 4*b = 40 + 4*3 = 40+12 = 52 м - периметр - ОТВЕТ 2
