Question

Здравствуйте,
необходимо найти область определения функции.
Фото прикрепляю ниже:

Answer 1

область определения это все допустимы значения х

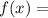
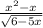
a)$f(x)=$$\frac{x^{2} -x}{\sqrt{6-5x} }$

дана дробь, в которой знаменатель имеет переменную х ,а также в знаменателе имеется корень⇒ знаменатель не может быть отрицательным ( так как вычленять из под корня отрицательные значения нельзя) и не может быть равен нулем(делить на ноль нельзя)

получаем  

√(6x-5)>0

6x-5>0

6x>5

x  ∈  (1.2;∞) ⇒ область определения (1.2;∞)

b)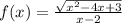$f(x)=\frac{\sqrt{x^{2}-4x+3 } }{x-2}$

тут тоже самое но √(x²-4x+3)≥0 (так как вычленять из под корня отрицательные значения нельзя)

x-2≠0 (делить на ноль нельзя)

x-2≠2 ⇒x≠2 ⇒  x ∈   (-∞;2) ∪ (2;∞)

√(x²-4x+3)≥0

x²-4x+3≥0

a=1>0 ⇒ интервал знакопостоянства таков

+  корень уравнения   -    корень уравнения    +

x²-4x+3=0

D=(-4)²-4×3×1=4

x=(4±√4)÷2=1  и 3

учитывая интервал и нестрогое неравенство

⇒ x ∈ (-∞;1] ∪ [3;∞)

теперь находим область определения

(  (-∞;1] ∪ [3;∞)  )   ∩    ( (-∞;2) ∪ (2;∞) ) = (-∞;1] ∪ [3;∞)

область определения  (-∞;1] ∪ [3;∞)

c)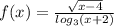$f(x)=\frac{\sqrt{x-4} }{log_{3} (x+2)}$

тут уже логарифмы результат логарифмы не должен быть 0 а значит

х+2≠1  ⇒х≠2  ⇒ х ∈ ( -∞;-1) ∪ (-1;∞)

в числителе корень значит

√(х-4)≥0

x-4≥0

x ∈  [4;∞)

ищем область определения

[4;∞)  ∩  ( ( -∞;-1) ∪ (-1;∞) ) = [4;∞)

область определения   [4;∞)