Пошаговое объяснение:
Поскольку касательные перпендикулярны радиусу в точке касания, то треугольники ОАС и OBD прямоугольные. Рассмотрим их. Здесь:
- АО=ВО как радиусы окружности;
- <COA=<DOB как вертикальные углы.
Используем один из признаков равенства прямоугольных треугольников: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Значит, в равных треугольниках ОАС и OBD равны и их гипотенузы. ОС=OD.
7
Пошаговое объяснение:
|x²–2·x–3|=3·x–3 ⇔ |(x+1)·(x–3)|=3·x–3.
Рассмотрим функцию под знаком модуля
y=(x+1)·(x–3)
Нули функции x₁ = –1 и x₂ = 3. Тогда эти точки делят ось Ох на промежутки (–∞; –1), (–1; 3) и (3; +∞), в которых функция сохраняет свой знак. Определим знаки функции:
1) x∈(–∞; –1): y=(x+1)·(x–3)>0, например: y(–2)=(–2+1)·(–2–3)=(–1)·(–5)=5>0
2) x∈(–1; 3): y=(x+1)·(x–3)<0, например: y(0)=(0+1)·(0–3)= 1·(–3)= –3<0
3) x∈(3; +∞): y=(x+1)·(x–3)>0, например: y(4)=(4+1)·(4–3)=5·1=5>0.
Теперь решаем неравенство.
1) Пусть x∈(–∞; –1]∪[3; +∞). Тогда (x+1)·(x–3)≥0 и по определению модуля
|x²–2·x–3|=x²–2·x–3. В силу этого:
x²–2·x–3=3·x–3 ⇔ x²–5·x=0 ⇔ (x–5)·x=0 ⇔
⇔ x₁ = 0 ∉(–∞; –1]∪[3; +∞) и x₂ = 5 ∈(–∞; –1]∪[3; +∞).
2) Пусть x∈(–1; 3). Тогда (x+1)·(x–3)<0 и по определению модуля
|x²–2·x–3|= –(x²–2·x–3). В силу этого:
x²–2·x–3= –(3·x–3) ⇔ x²+x–6=0 ⇔ (x–2)·(x+3)=0 ⇔
⇔ x₃ = 2 ∈(–1; 3) и x₄ = –3 ∉(–1; 3).
Тогда сумма корней уравнения:
5 + 2 = 7.
Пусть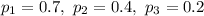
- вероятности попадания бомб
Тогда,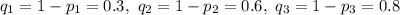
- вероятности промаха соответственно
Значит, в случае одного попадания мост разрушится с вероятностью:
В случае двух попадания мост разрушится с вероятностью:
В случае трех попадания мост разрушится с вероятностью:
Все три события несовместны, поэтому общая вероятность разрушения равна сумме трех предыдущих вероятностей:
ответ: 0.56