В чашке было 3 л в другогом на 1 л больше Сколько литров кофе в двух чашках

👇

Увидеть ответ

Ответ:

Александрик397

30.06.2022

В 1 чашке - 3л

Во 2 чашке - ?, на 1л больше

В двух чашках - ?л

1) 3+1=4л ( во 2 чашке)

2) 4+3=7л ( в двух чашках)

ответ: 7л в двух чашках

4,6(37 оценок)

Ответ:

9109160145davla

30.06.2022

7л

Пошаговое объяснение:

1ч=3л

2ч=3+1=4л

1ч+2ч=3л+4л=7л

4,4(65 оценок)

Открыть все ответы

Ответ:

Dizzy234

30.06.2022

1.А) Уравнением называется равенство, содержащее одно или несколько неизвестных, значение которых необходимо найти.

2. верный ответ Значение переменной, при котором уравнение обращается в верное равенство.

среди предложенных не нашел.

3. линейным называют уравнение, в котором переменная /или переменные/ входят в первой степени, не равны нулю. можем еще так сказать

это уравнение вида ах+b=c

ax+by=c , где a, b, c - некоторые числа, х и у -переменные. причем а≠0, если речь об уравнении с двумя переменными, то а≠0;b≠0.

4. квадратное - это уравнение вида ах²+bx+c=0, где а,b,с - некоторые числа, причем а≠0, х и у-переменные.

5. Неравенство вида ах+b<0 (ах+b≤0, ах+b>0, ах+b≥0).где а≠0.

6. А) Уравнение имеет два равных действительных корня. но при условии, что решаем уравнение в области действительных чисел. иначе ответ Е.

7. А) Уравнение имеет два различных действительных корня. если речь о решении кв. уравнения в области действительных чисел.

иначе ответ Е.

8. А) Уравнение не имеет действительных корней.

9.D=b²-4ас

10. А) Уравнения, имеющие одно и то же множество решений

11. 7х-8=2х-3⇒А)х=1

12. 3-4х=5+8х⇒12х=-2, х=-1/6, верного ответа нет.

13. 7-х=-4+10х; х=1

14. 4х-4=6+3х⇒А)х=10

15. А) -0.5

16. 7-3х-3=х-1⇒А)1.25

17. -15+3х=2х-19⇒А)-4

18. 3-2х<5-3х⇒А) x<2

19. 5х+6>3х-2⇒А) x>-4

20. 3х-5≥23-4х⇒А) x≥4

21. По Виету А) 4;-2

22. 3х²-2х-1=0−1

здесь два ответа . ноль и 2/3

23. у=х+1 целая прямая ответов. подходят А, С,

24.- нет системы

25.аналогично.

26. аналогично

27 нет

28. 10х²-х+1=0 А) Не имеет действительных корней

29 нет уравнения

30нет неравенства. но больше половины, как требуют правила, я решил вам.

4,4(68 оценок)

Ответ:

viktoriya2000ok

30.06.2022

Будем разбивать на несколько случаев.

1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 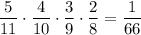$\dfrac{5}{11}\cdot \dfrac{4}{10}\cdot \dfrac{3}{9}\cdot\dfrac{2}{8}=\dfrac{1}{66}$ . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна $\dfrac{3}{12}\cdot\dfrac{2}{11}\cdot\dfrac{1}{10}=\dfrac{1}{220}$ . 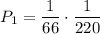По теореме умножения $P_1=\dfrac{1}{66}\cdot\dfrac{1}{220}$

2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 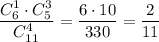$\dfrac{C^1_6\cdot C^3_5}{C^4_{11}}=\dfrac{6\cdot10}{330}=\dfrac{2}{11}$ . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 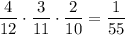$\dfrac{4}{12}\cdot\dfrac{3}{11}\cdot\dfrac{2}{10}=\dfrac{1}{55}$ . По теореме умножения: $P_2=\dfrac{2}{11}\cdot\dfrac{1}{55}$

3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 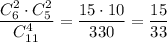$\dfrac{C^2_6\cdot C^2_5}{C^4_{11}}=\dfrac{15\cdot10}{330}=\dfrac{15}{33}$ . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 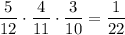$\dfrac{5}{12}\cdot\dfrac{4}{11}\cdot\dfrac{3}{10}=\dfrac{1}{22}$ . По теореме умножения : $P_3=\dfrac{15}{33}\cdot\dfrac{1}{22}$

4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна $\dfrac{C^3_6\cdot C^1_5}{C^4_{11}}=\dfrac{20\cdot5}{330}=\dfrac{10}{33}$ . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна $\dfrac{6}{12}\cdot\dfrac{5}{11}\cdot\dfrac{4}{10}=\dfrac{1}{11}$ . 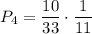По теореме умножения: $P_4=\dfrac{10}{33}\cdot\dfrac{1}{11}$

5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 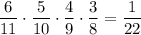$\dfrac{6}{11}\cdot\dfrac{5}{10}\cdot\dfrac{4}{9}\cdot\dfrac{3}{8}=\dfrac{1}{22}$ . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 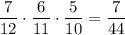$\dfrac{7}{12}\cdot\dfrac{6}{11}\cdot\dfrac{5}{10}=\dfrac{7}{44}$ . По теореме умножения: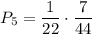 $P_5=\dfrac{1}{22}\cdot\dfrac{7}{44}$

Итого, по теореме сложения:

$P=P_1+P_2+P_3+P_4+P_5=\dfrac{1}{66}\cdot\dfrac{1}{220}+\dfrac{2}{11}\cdot\dfrac{1}{55}+\dfrac{15}{33}\cdot\dfrac{1}{22}+\\ \\ +\dfrac{10}{33}\cdot\dfrac{1}{11}+\dfrac{1}{22}\cdot\dfrac{7}{44}=\dfrac{427}{7260}\approx 0{,}0588$