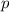и 
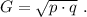
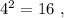а произведение двух самых больших равно 
»
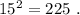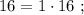
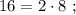
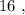т.е.: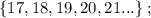 
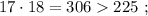
каждое – будет, очевидно, больше чем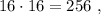 
т.е. больше 
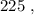а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.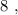
т.е.: 
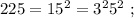
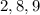и 
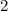и 
и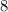 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы 
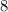и никаких натуральных чисел нет. и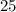 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 
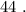
Понятно, что мистер Фокс может выложить в ряд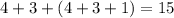
предметов (К - карандаш, Л = ластик, Т = точилка):
К Л К Л К Л К Л К Т К Т К Т К.
Теперь докажем, что больше, чем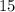
предметов, в ряд выложить мистер Фокс не сможет. Если не так, то было выложено всего хотя бы 
карандашей. И, чтобы, никакие два одинаковых предмета не были рядом, между карандашами должно быть хотя бы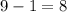 
инородных предметов. А их у нас всего-то 
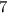. Обратите внимание, что 
.
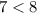Значит, наибольшее возможное число предметов в ряду - это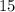
.
ответ: