1б.=8, 2б.=16, 3б.=21
Пошаговое объяснение:
пускай 1б- х, 2б- х+8, 3б- х+8+5, тогда:
х+х+8+5+х+8=45
3х+21=45
3х=45-21
3х=24
х=24:3
х=8 (л) - 1б
8+8= 16 (л) - 2б
16+5=21 (л) - 3б
Пошаговое объяснение:
ищем определитель через разложение по 1-му столбцу:
2 1 -1
Δ₁₁= 2 -1 3
0 1 2
определитель для этого минора.
∆₁₁ = 2*((-1)*2-1*3)-2*(1*2-1*(-1))+0*(1*3-(-1)*(-1)) = -16
минор для (2,1):
-1 0 3
Δ₂₁= 2 -1 3
0 1 2
определитель для этого минора.
∆₂₁ = (-1)*((-1)*2-1*3)-2*(0*2-1*3)+0*(0*3-(-1)*3) = 11
минор для (3,1):
-1 0 3
∆₃₁ = 2 1 -1
0 1 2
определитель для этого минора.
∆3,1 = (-1)*(1*2-1*(-1))-2*(0*2-1*3)+0*(0*(-1)-1*3) = 3
минор для (4,1):
-1 0 3
Δ₄₁ = 2 1 -1
2 -1 3
определитель для этого минора.
∆₄₁ = (-1)*(1*3-(-1)*(-1))-2*(0*3-(-1)*3)+2*(0*(-1)-1*3) = -14
определитель матрицы
∆ = (-1)⁽¹⁺¹⁾ *1*(-16) + (-1)⁽²⁺¹⁾ *3*11 + (-1)⁽³⁺¹⁾ *1*3 + (-1)⁽⁴⁺¹⁾ *4*(-14) = 10

Пошаговое объяснение:
11. На рисунке изображено 2 прямоугольных треугольника.
Рассмотрим меньший треугольник. Его гипотенуза равна 2, а один из катетов равен "х". Обозначим другой катет как "у". Тогда, по теореме Пифагора, для этого треугольника справедливо равенство

Рассмотрим больший треугольник. Один катет равен "у", а другой катет равен "х+2". По аналогии с предыдущим треугольником, получаем:

Получено 2 уравнения с двумя переменными. Запишем и решим систему уравнений:

Избавимся от слагаемого y². Для этого выполним почленное вычитание двух уравнений:

Квадрат суммы двух выражений раскрывается по следующей формуле:

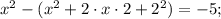

Если перед скобкой стоит знак "–", то знаки слагаемых, находящихся в скобке, меняются на противоположные:


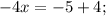
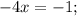
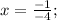
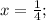
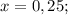
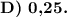
Пошаговое объяснение:
1-x
2-x+8
3-x+5+8
x+x+8+x+5+8=45
3x=45-5-16
3x=24
x=8
1-8 литров
2-16литров
3-21литров