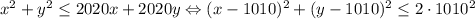, то есть это круг (с границей), с центром в точке 
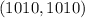и радиусом 
. Среди точек этого множества требуется найти такие, для которых 
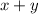принимает наибольшее значение. Понятно также, что никакая точка внутренности не является искомой, поскольку ее можно сдвинуть на вектор 
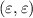для некоторого 
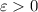. Потому точки ищем на границе.
Рассмотрим прямую 
. Требуется максимизировать 
, то есть увеличивать это значение до тех пор, пока эта прямая имеет пересечения с окружностью. Предельный случай -- касание. Имеем: 
, 
, откуда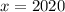 
. Тогда 
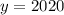и 
.
Пошаговое объяснение:
Δ
и Δ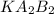
подобны по второму признаку:
Из свойства накрест лежащих углов полученные при пересечении секущей имеем что углы ∠
и ∠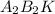
равны. Так же равны накрест лежащие углы ∠
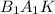и ∠
.
Из подобия треугольников Δ
и Δ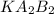
следует пропорциональность сторон 
. Обозначим 
, тогда 
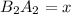и 
. Подставив в пропорцию 
и учитывая последнее в пропорцию выше имеем следующее уравнение:
откуда имеем, что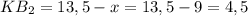
.