Среднее арифметическое трёх чисел — 15. Найди эти числа, если первое число в 2,5 раза больше третьего, а второе в 1,5 раз(-а) больше третьего.

👇

Увидеть ответ

Ответ:

sabinabaigali

17.05.2020

Составим уравнение

$\frac{2,5x+1,5x+x}{3} =15\\2,5x+1,5x+x=45\\5x=45\\x=9$

3-е число - 9, значит 1-ое число 9*2,5=22,5; а 2-ое число 9*1,5=13,5

1-ое число - 22,5;

2-ое число - 13,5;

3-е число - 9.

4,4(67 оценок)

Открыть все ответы

Ответ:

игорь780

17.05.2020

Скорость в гору 12 км/ч, скорость под гору 30 км/ч

Пошаговое объяснение:

34. Путь от А до в идет сначала 3км вверх, а затем 6км под гору и 12 км по pовному месту. Этот путь мотоциклист проехал за 1 час 7 мин, а обратный путь он проехал за 1 час 16мин. Найти скорость мотоциклиста в гору и скорость под гору, если по равнине он ехал со скоростью 18 км/ час.

Движение из пункта А.

х - скорость мотоциклиста в гору

3/х - время движения мотоциклиста в гору

у - скорость мотоциклиста под гору

6/у - время движения мотоциклиста под гору

12/18 = 2/3 часа- время движения мотоциклиста по равнине

Всё время движения из А определяется уравнением

$\dfrac{3}{x} + \dfrac{6}{y} + \dfrac{2}{3} = 1\dfrac{7}{60}~~~~~~~(1)$

Движение обратно в пункт А: движение в гору становится движением под гору и наоборот.

Всё время движения в А определяется уравнением

$\dfrac{3}{y} + \dfrac{6}{x} + \dfrac{2}{3} = 1\dfrac{16}{60}~~~~~~~(2)$

Из уравнения (1) получим

$\dfrac{3}{x} + \dfrac{6}{y} = \dfrac{9}{20}~~~$

Из уравнения (2) получим

$\dfrac{6}{x} +\dfrac{3}{y} =\dfrac{12}{20}$

Решаем систему уравнений

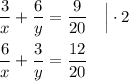
$\dfrac{3}{x} + \dfrac{6}{y} = \dfrac{9}{20}~~~\Big |\cdot 2\\ \\\dfrac{6}{x} +\dfrac{3}{y} =\dfrac{12}{20}$

$\dfrac{6}{x} + \dfrac{12}{y} = \dfrac{18}{20}\\ \\\dfrac{6}{x} +\dfrac{3}{y} =\dfrac{12}{20}$

Вычитаем из 1-го уравнения 2-е

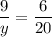
$\dfrac{9}{y} = \dfrac{6}{20}$

у = 30 (км/ч)

Из (1)

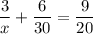
$\dfrac{3}{x} + \dfrac{6}{30} = \dfrac{9}{20}~~~$

Получим

$\dfrac{3}{x} = \dfrac{1}{4}~~~$

х = 12 (км/ч)

4,5(85 оценок)

Ответ:

tvzhanna80

17.05.2020

Модуль числа также принято называть абсолютной величиной этого числа. Он обозначается короткими вертикальными линиями, проведенными слева и справа от числа. Например, модуль числа 15 записывается следующим образом: |15|.Помните, что модуль может быть только положительным числом или нулем. Модуль положительного числа равен самому числу. Модуль нуля равен нулю. То есть для любого числа n, которое больше либо равно нулю, будет справедлива следующая формула |n| = n. Например, |15| = 15, то есть модуль числа 15 равен 15-ти.Модулем отрицательного числа будет то же число, но с противоположным знаком. То есть для любого числа n, которое меньше нуля, будет справедлива формула |n| = -n. Например, |-28| = 28. Модуль числа -28 равен 28-ми.Можно находить модули не только для целых, но и для дробных чисел. Причем в отношении дробных чисел действуют те же правила. Например, |0,25| = 25, то есть модуль числа 0,25 будет равен 0,25. А |-¾| = ¾, то есть модуль числа -¾ будет равен ¾.При работе с модулями полезно знать, что модули противоположных чисел всегда равны друг другу, то есть |n| =|-n|. Это является основным свойством модулей. Например, |10| = |-10|. Модуль числа 10 равен 10-ти, точно так же, как модуль числа -10. Кроме того, |a - b| = |b - a|, так как расстояние от точки a до точки b и расстояние от b до a равны друг другу. Например, |25 - 5| = |5 - 25|, то есть |20| = |- 20|.

4,4(42 оценок)

Это интересно:

Питомцы-и-животные

30.03.2021

Как правильно ухаживать за ежиком: досье на пушистых игривых существ...

Компьютеры-и-электроника

30.07.2021

Как вернуть старый аккаунт на Neopets: полное руководство...

Дом-и-сад

18.10.2021

Как убить домашних жуков: лучшие способы и средства борьбы...

Компьютеры-и-электроника