
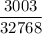
Пошаговое объяснение:
Пусть в каждом гардеробе было по 15 мест, представим гардероб как последовательность нулей и единиц: 0 — школьник разделся в другом гардеробе, 1 — школьник разделся в этом гардеробе. Тогда ситуация выглядит примерно так:
I: 110010100011101
II: 001101011100010
Если в первом гардеробе задана некоторая последовательность, то она однозначно задаёт последовательность второго гардероба. На каждой позиции первого гардероба может быть либо 0, либо 1, поэтому, учитывая однозначность, всего возможных ситуаций 2¹⁵ = 32768.
Если в правом гардеробе занято вдвое мест, чем в левом, то есть вдвое больше единиц, чем в левом (10 в правом, 5 в левом), то искомое количество подходящих ситуаций — число расставить 10 единиц в правом гардеробе.
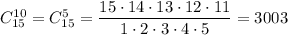
Искомая вероятность равна 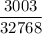 .
.
Пусть Коля купил х пирожков, тогда Вася 2х пирожков, а Женя у пирожков, причем х < y < 2x
Составим уравнение: х + 2х + у = 14;
3х + у = 14
3х = 14 - у.
Выражение 14 - у должно делиться на 3: числа до 14, делящиеся на 3 - это 12, 9, 6, 3.
Исследуем все варианты:
1) 14 - у = 12, тогда у = 2; 3х = 12; х = 4; 2х = 8; 4 < 2 < 8 (ложь)
2) 14 - у = 9, тогда у = 5; 3х = 9; х = 3; 2х = 6; 3 < 5 < 6 (истина)
3) 14 - у = 6, тогда у = 8; 3х = 6; х = 2; 2х = 4; 2 < 8 < 4 (ложь)
4) 14 - у = 3, тогда у =11; 3х = 3; х = 1; 2х = 2; 1 <11 < 2 (ложь)
Видим, что подходит только вариант 2), следовательно, Коля купил 3 пирожка, Вася 6 пирожков, а Женя 5 пирожков.
Пошаговое объяснение: