Пошаговое объяснение:
Чтобы решить систему уравнений, надо одну из переменных выразить через другую и подставить полученное выражение во второе уравнение:
2 – 3 * х = 2 * (1 - у);
2 – 3 * х = 2 – 2 * у;
-3 * х = - 2 * у;
у = - 3 * х / -2 = 3 * х / 2.
Подставим во второе уравнение полученное выражение:
4 * (х + у) = х – 1,5;
4 * (х + (3 * х / 2)) – х + 1,5 = 0;
4 * х + 6 * х – х + 1,5 = 0;
9 * х + 1,5 = 0;
9 * х = - 1,5;
х = - 1,5 / 9 = - 15 / 90 = - 1/6.
у = 3 * х / 2 = 3 * (- 1/6) / 2 = - (1/2) / 2 = - 1/4 = - 0,25.
ответ: решением системы уравнений является пара чисел: х = -1/6; у = -0,25.
(x+5)^3 > 8 .Можем извлечь из 3 степени ,т.к. степень нечетная и знак не поменяет ,тогда x+5 > 2 , x > -3
ответ : x∈ (-3;+∞)
2) (3x - 5 ) ^ 7 < 1. Можем извлечь из 7 степени ,т.к. степень нечетная и знак не поменяет ,тогда 3x- 5 < 1 ; 3x < 6 ; x<2
ответ : x∈ (-∞;2)
3) (4 - x)^4 > 81 . т.к. степень четная ,то при извлечении из 4 степени ,нужно добавить модуль ,т.е. |4-x| > 3 . Разобьем на две системы неравенств :
.Решение первого неравенства (-∞;1) ,а второго (7;+∞) . Объединяя получаем ,что x∈(-∞;1) V (7;+∞)
ответ: x∈(-∞;1) V (7;+∞)
1) 0=x+2 +4x-7
x=1
2) 0=2x^3 - 3x^2 +1
x1= -1/2, x2=1
x1= - 0,5, x2=1
3) y-9 = -x^2+6x-9 -5
y-9 = - (x^2-6x+9) -5
y-9 = - (x-3)^2-5
y= - (x+3)^2 -5 +9
y= -(x-3)^2+4
4) 0=x^3 +3x^2 - 9x
x1 =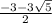
, x2 = 0, x3 =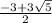 
x1 = - 4,8541, x2=0, x3= 1,8541
5) 0 = x^4-2x^2-3
x1 = -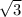
, x2=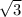 
x1= -1,73205, x2= 1,73205
6) y=0^3 + 4 * 0-8
y=-8
7) y=0^4-8*0-9
y=9
8) y=9+4*0^3-0^4
y=9
9) y+100=x^2-20x+100
y+100=(x-10)^2
y= (x-10)^2-100
10) 0=cos(x)
x=π/2 + kπ, k ∈ Z
Пошаговое объяснение: