Пусть еще не все числа нули.
Выбираем одно положительное число, одно отрицательное и 299 любых других чисел (если все числа были бы одного знака и хотя бы одно отличалось от нуля, то сумма не могла бы быть равна нулю, так что такой выбор всегда возможен).Берем положительное число и выбранные 299 чисел. Вычитаем из них 1.Берем отрицательное число и выбранные 299 чисел. Меняем им знак, вычитаем из них 1, опять меняем знак.В результате изменятся только выбранное отрицательное и выбранное положительное числа: к отрицательному будет прибавлено 1, из положительного - вычтено 1. Каждое из 299 чисел не меняется:
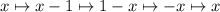
Сумма не поменяется, так что такие действия можно продолжать до тех пор, пока все числа не станут нулями.
Процесс завершится за конечное число шагов: действительно, на каждом шаге сумма модулей всех чисел - неотрицательное целое число - уменьшается на 2, поэтому, если сумма модулей исходных чисел равна 2S, за S итераций сумма модулей станет равна 0, что возможно, только если все числа - нули.
=(16,25- 2,45+2,7*(-20/3)+3 7/15=(16,25- 2,45+0,9*(-20/1)+3 7/15=
=(16,25- 2,45+(-18)+3 7/15=
№2) (5,2+1 3/7)²= (5 2/10+1 3/7)²= (5 1/5+1 3/7)²= (5 7/35+1 15/35)²=
=(6 22/35)²= (232/35)²=53824/1225=43 1149/1225
№3) 2 1/6 у-0,22=2,4 у-8/25
2 1/6у-2,4у=-8/25+0,22
2 1/6у-2 4/10у=-0,32+0,22
2 1/6у-2 2/5у=-0,1
2 5/30у-2 12/30у=-0,1
5/30у- 12/30у=-1/10
-7/30у=-1/10
7/30у=1/10
у=1/10:7/30
у=1/10*30/7
у=1/1*3/7
у=3/7
№4) 6(4-3 х )=43-5(4+3 х )
24-18х=43-20+3х
24-18х=23+3х
-18х-3х=23-24
-21х=-1
21х=1
х=1/21