1 сторона-20см 2 сторона-18см 3 сторона-14 см
Пошаговое объяснение:
Дано:
(O;r) ∆АВС. M,K, F - точки
Р∆АВС = 52 см. AM : MB = 2 : 3. KC = 6 см.
рішення
нехай одна сторона=x см,тогда AM=2x,MB=3x.
MB=BK=3х(по св-ву отрезков касательной)
AM=AF=2x(по св-ву отрезков касательной)
FC=KC=6 см(по св-ву отрезков касательной)
AB=MB+AM=3x+2x=5x
BC=6+3x
AC=6+2x
Складаємо рівняння
5х + 3х + 6 + 2х + 6 = 52
10х + 12 = 52
10х = 51 - 12
10х = 40
х = 4
одна сторона-4см
АВ = 5 * 4 = 20 см;
ВС = 3 * 4 + 6 = 18 см;
АС = 2* 4 + 6 = 14 см.
А)8см і 18см.
Г)10см і 18 см.
Пошаговое объяснение:
1) Пусть АЕ - биссектриса острого угла параллелограмма АВСD, тогда ∠1 = ∠2.
2) ∠2 = ∠3 (накрест лежащие при ВС ll AD и секущей АЕ). Получили, что
∠1 = ∠3, тогда ∆АВЕ равнобедренный по признаку, АВ = ВЕ.
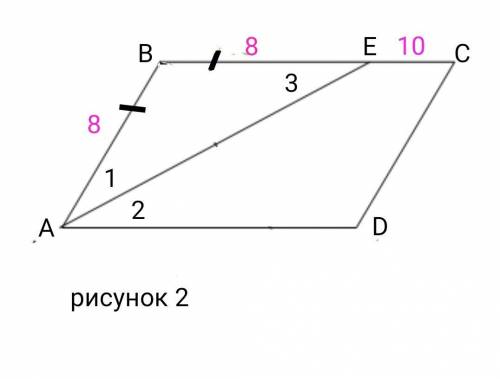
3) Возможны два случая.
1случай (рис. 1): ВЕ = 10 см и ЕС = 8 см .
В этом случае
ВС = ВЕ + ЕС = 18 (см), АВ = ВЕ = 10 см,
ответ: стороны параллелограмма равны 10 см и 18 см.
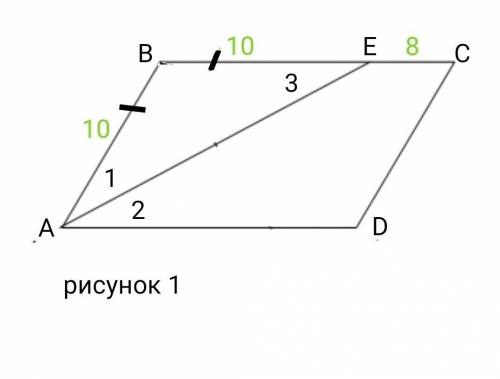
2 случай (рис. 2): ВЕ = 8 см и ЕС = 10 см .
В этом случае
ВС = ВЕ + ЕС = 18 (см), АВ = ВЕ = 8 см,
ответ: стороны параллелограмма равны 8 см и 18 см.
берем производную:
f(x)'=2(3x^2)-6=6x^2-6
ищем экстремиумы:
6x^2-6=0; x^2=1; x1=1; x2=-1
y1=0, y2=8;
у функции 2 экстремиума: (1;0) и (-1;8)
определяем методом интервалов возрастание/убывание:
возрастает: x=(-беск;-1] и [1;+беск)
убывает: x= [-1;1]
определаяем четность/нечетность:
f(-x)=2(-x)^3-6(-x)+4=-2x^3+6x+4=-(2x^3-6x-4) - функция не является ни четной ни нечетной;
ищем точки перегиба:
берем 2 производную:
f(x)''=6(2x)=12x
12x=0; x=0;
y=4; (0;4)
методом интервалов находим выпуклость/ вогнутсть:
выпукла: (-беск;0]
вогнута: [0;+беск)
собираем точки:
(1;0), (-1;8), (0,4)
и по ним строим график: