1. Длина окружности может быть определена по формуле:
C = π*d = 3,14*35 = 109,9 см
где d – диаметр.
2. Масштаб 1:1000 подразумевает, что на карте все линейные размеры уменьшены в 1000 раз по сравнению с реальными. Отсюда:
L = 9,6*1000 = 9600 см или 96 м
3. Площадь круга может быть определена по формуле
S = π*r^2 = π*7^2 = 3,1*49 = 151.9 дм^2
где r – радиус.
4. Процент снижения цены товара определится:
p = 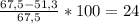
5. Площадь прямоугольника определяется по формуле:
S = a*b
где a, b – стороны.
Каждая сторона в 500 раз больше, чем на плане (см. задачу 2), таким образом, реальная площадь прямоугольного участка:
Sр = 500*a*500*b = 250000*S = 250000*25 = 6250000 см^2 или 625 м^2
ответ1:
1. Проведи в грани ВВ1С1С диагональ ВС1. Эта диагональ - есть проекция наклонной АС1 на плоскость ВВ1С1С.
2. Согласно теореме о наклонной угол АВС1 - искомый угол между прямой AC1 и плоскостью BCC1. Обозначим его через г.
3. Рассмотрим треугольник АВС1. Так как АВ перпендикулярно ВС и перпендикулярно ВВ1, то АВ перпендикулярно BCC1. (теорема есть такая)
4. Следовательно, треугольник АВС1 - прямоугольный со всеми вытекающими отсюда последствиями.
5. Обозначим ребро куба через а. Тогда АС1 = а*корень (3) - диагональ куба. И ВС1 = а*корень (2) - диагональ квадрата ВВ1С1С.
6. Тогда в прямоугольном треугольнике АВС1--- косинус (г) = ВС1/АС1=корень (2/3). Отсюда: г = арккосинус ( корень (2/3)).
ответ 2:
Угол между прямой и плоскостью - это угол между прямой и её проекцией на эту плоскость. Проекция - это отрезок между точкой пересечения прямой с плоскостью и основанием перпендикуляра к плоскости. На рисунке первого ответа видно, что С1D1 это перпендикуляр к плоскости АА1D1 так как он перпендикулярен двум пересекающимся прямым этой плоскости. Значит искомый угол - это угол С1АD1