Натуральные числа - это числа, которые используются для счёта предметов (1, 2, 3 ...). n - первое натуральное число n + 1 - второе натуральное число n + 2 - третье натуральное число n + 3 - четвёртое натуральное число Уравнение: (n + 2) * (n + 3) - n * (n + 1) = 58 n^2 + 2n + 3n + 6 - n^2 - n = 58 (n^2 - n^2) + (2n + 3n - n) + 6 = 58 4n + 6 = 58 4n = 58 - 6 4n = 52 n = 52 : 4 = 13 - первое число 13 + 1 = 14 - второе число 13 + 2 = 15 - третье число 13 + 3 = 16 - четвёртое число ответ: 13, 14, 15, 16.
см ниже
Пошаговое объяснение:
№1
а) 14/6= 7/3= 2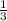 ;
;
б) 100/3= 33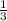 ;
;
в) 43/10= 4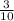 ;
;
г) 78/17= 4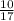 ;
;
д) 917/11=83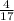
№2
аb/c = (ac+b)/c
а)7 1/8 = (7*8+1)/8=57/8;
б) 3 4/5=(3*5+4)/5=19/5;
в) 1 7/10= (1*10+7)/10= 17/10;
г) 9 14/15= (9*15+14)/15=149/15;
д) 5 3/16= (5*16+3)/16=83/16
№3
со знаменателем 4
а) 28/4, 36/4, 40/4 ;
со знаменателем 5
б) 10/5, 15/5, 40/5
№4
9 2/3 : 1/3 = ((9*3+2)*3)/(3*1) = 29 получилось таких частей
№5
a) 132/k = 11
k = 132/11
k = 12
б) 56/(48-(2х-6)) = 14
48-(2х-6) = 56/14
48-2х+6 = 4
-2х = 4 -48-6
-2х = -50
2х = 50
х = 50/2
х = 25
№6
(4а+3)/12
4а+3 < 12
4а < 12-3
4а < 9
а < 9/4
а < 2 1/4
при a=1 или а=2 дробь будет правильной
21 > 6а+2
6а<21-2
6а<19
а<19/6
а<3 1/6
при a=1 или а=2 или а=3 Дробь 21/(6а+2) будет неправильной