Если существует предел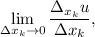 
то этот предел называется частной производной от функции 
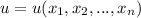по переменной 
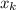и обозначается 
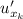или 
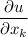
Для функции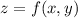 
следует найти частные производные 
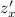и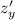 
Для нахождения таких производных по данной переменной следует все переменные, кроме данной, считать константами (числами).
Например, для функции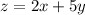 
частной производной функции по переменной 
будет: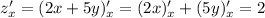 
(считаем выражение 
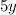числовым, производная от которого равна нулю), и аналогично по переменной 
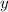будет: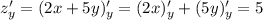 
Для заданной функции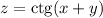 
найдем частные производные 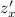и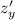
Воспользуемся формулой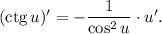 
Имеем:
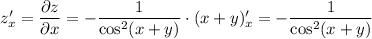
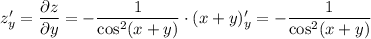
ответ: 
3. Задание: Найти сколько килограммов картофеля осталось в магазине
Решение: 800:100*60 = 480 кг.
ответ: 480 кг.
4. Задание: Округлить ответы до сотых и вычислить их среднее арифметическое
8 м 7 см 3 мм = 8,073 м ≈ 8, 070 м
47 см 6 мм = 0,476 м ≈ 0,480 м
25 мм = 0,025 м. ≈ 0,030 м
(8,070 + 0,480 + 0,030) : 3 = 2,86м
ответ: 2,86 м
5. Задание: Найти объём образованного параллелепипеда.
Решение: 30*20*10 = 6000 см³
ответ: 6000 см³